100. Same Tree

Given the roots of two binary trees p and q, write a function to check if they are the same or not.

Two binary trees are considered the same if they are structurally identical, and the nodes have the same value.

Example 1:

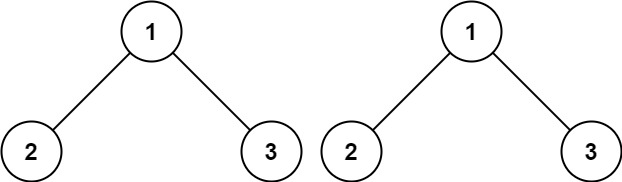
Input: p = [1,2,3], q = [1,2,3]
Output: true

Example 2:

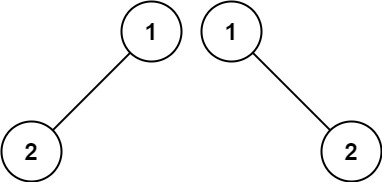
Input: p = [1,2], q = [1,null,2]
Output: false

Example 3:

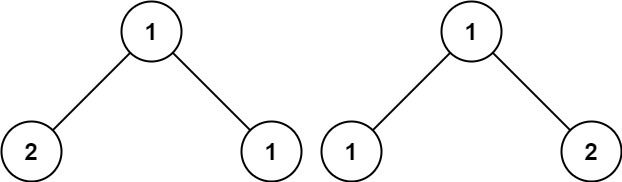
Input: p = [1,2,1], q = [1,1,2]
Output: false

Constraints:

• The number of nodes in both trees is in the range [0, 100].
• -104 <= Node.val <= 104

Approach 01:

#include <bits/stdc++.h>

using namespace std;

struct TreeNode {
      int val;
      TreeNode *left;
      TreeNode *right;
      TreeNode() : val(0), left(nullptr), right(nullptr) {}
      TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
      TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
  };
 
class Solution {
public:
    bool isSameTree(TreeNode *p, TreeNode *q) {
        if (p == nullptr && q == nullptr)
            return true;
        if (p == nullptr || q == nullptr)
            return false;
        if (p->val != q->val)
            return false;
        return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
    }
};

from typing import *

class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right
        
class Solution:
    def isSameTree(self, p: Optional[TreeNode], q: Optional[TreeNode]) -> bool:
        if(p is None and q is None):
            return True
        if(p is None or q is None):
            return False
        if(p.val != q.val):
            return False
        
        result = self.isSameTree(p.left, q.left) and self.isSameTree(p.right, q.right)
        return result

Time Complexity

• Recursive Traversal:

  The function isSameTree performs a recursive traversal of both trees. In the worst case, every node in both trees needs to be compared once.

• Overall Time Complexity:

  The overall time complexity is \( O(n) \), where \( n \) is the number of nodes in the smaller of the two trees.

Space Complexity

• Recursive Stack Space:

  The space complexity is determined by the maximum depth of the recursion stack. In the worst case, this depth is equal to the height of the tree.

• Overall Space Complexity:

  The overall space complexity is \( O(h) \), where \( h \) is the height of the tree. In the worst case, for a completely unbalanced tree, this can be \( O(n) \). For a balanced tree, the space complexity will be \( O(\log n) \).