1110. Delete Nodes And Return Forest

Given the root of a binary tree, each node in the tree has a distinct value.

After deleting all nodes with a value in to_delete, we are left with a forest (a disjoint union of trees).

Return the roots of the trees in the remaining forest. You may return the result in any order.

Example 1:

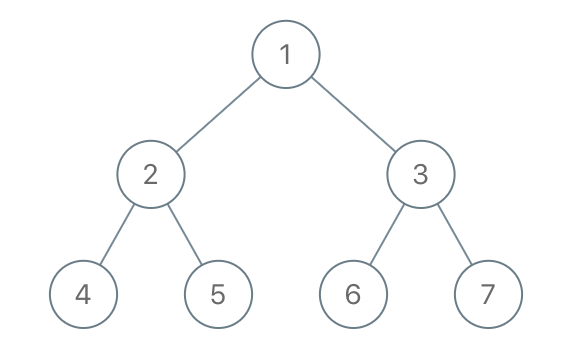
Input: root = [1,2,3,4,5,6,7], to_delete = [3,5]
Output: [[1,2,null,4],[6],[7]]

Example 2:

Input: root = [1,2,4,null,3], to_delete = [3]
Output: [[1,2,4]]

Constraints:

• The number of nodes in the given tree is at most 1000.
• Each node has a distinct value between 1 and 1000.
• to_delete.length <= 1000
• to_delete contains distinct values between 1 and 1000.

Approach01:

#include <bits/stdc++.h>

using namespace std;

class Solution {
public:
    vector<TreeNode*> delNodes(TreeNode* root, vector<int>& to_delete) {
        vector<TreeNode*> remainingTrees;
        // Create a set from to_delete vector for quick lookup
        unordered_set<int> toDeleteSet(to_delete.begin(), to_delete.end());
        // Start the DFS removal process
        removeNodes(root, toDeleteSet, true, remainingTrees);
        return remainingTrees;
    }

private:
    // Helper function to perform DFS and remove nodes
    TreeNode* removeNodes(TreeNode*& node, const unordered_set<int>& toDeleteSet, bool isRoot, vector<TreeNode*>& remainingTrees) {
        if (node == nullptr){
            return nullptr;
        }

        // Check if the current node needs to be deleted
        const bool isDeleted = toDeleteSet.count(node->val) > 0;

        // If the current node is a root and not deleted, add it to the result
        if (isRoot && !isDeleted){
            remainingTrees.push_back(node);
        }

        // Recursively process the left and right subtrees
        node->left =  removeNodes(node->left, toDeleteSet, isDeleted, remainingTrees);
        node->right = removeNodes(node->right, toDeleteSet, isDeleted, remainingTrees);

        // Return nullptr if the node is deleted, otherwise return the node
        // itself
        return isDeleted ? nullptr : node;
    }
};

from typing import List, Optional, Set
from collections import deque

class Solution:
    def delNodes(self, root: Optional[TreeNode], to_delete: List[int]) -> List[TreeNode]:
        remaining_trees = []
        to_delete_set = set(to_delete)  # Create a set from to_delete list for quick lookup
        self.removeNodes(root, to_delete_set, True, remaining_trees)
        return remaining_trees

    def removeNodes(self, node: Optional[TreeNode], to_delete_set: Set[int], is_root: bool, remaining_trees: List[TreeNode]) -> Optional[TreeNode]:
        if node is None:
            return None

        # Check if the current node needs to be deleted
        is_deleted = node.val in to_delete_set

        # If the current node is a root and not deleted, add it to the result
        if is_root and not is_deleted:
            remaining_trees.append(node)

        # Recursively process the left and right subtrees
        node.left = self.removeNodes(node.left, to_delete_set, is_deleted, remaining_trees)
        node.right = self.removeNodes(node.right, to_delete_set, is_deleted, remaining_trees)

        # Return None if the node is deleted, otherwise return the node itself
        return None if is_deleted else node

Time Complexity

• Creating the toDeleteSet:

  Creating the toDeleteSet from the to_delete vector takes \( O(m) \) time, where \( m \) is the number of elements in the to_delete vector.

• DFS Traversal:

  The DFS traversal of the tree visits each node exactly once, resulting in \( O(n) \) time, where \( n \) is the number of nodes in the tree.

• Overall Time Complexity:

  The overall time complexity is \( O(m) + O(n) = O(n + m) \).

Space Complexity

• Auxiliary Space for toDeleteSet:

  The toDeleteSet stores up to \( m \) elements, resulting in \( O(m) \) space usage.

• Recursive Call Stack:

  The depth of the recursive call stack is proportional to the height of the tree, which in the worst case is \( O(n) \) for a skewed tree. For a balanced tree, it would be \( O(\log n) \).

• Overall Space Complexity:

  The overall space complexity is \( O(m + n) \) in the worst case.