1261. Find Elements in a Contaminated Binary Tree

Given a binary tree with the following rules:

1. root.val == 0
2. For any treeNode:
   1. If treeNode.val has a value x and treeNode.left != null, then treeNode.left.val == 2 * x + 1
   2. If treeNode.val has a value x and treeNode.right != null, then treeNode.right.val == 2 * x + 2

Now the binary tree is contaminated, which means all treeNode.val have been changed to -1.

Implement the FindElements class:

• FindElements(TreeNode* root) Initializes the object with a contaminated binary tree and recovers it.
• bool find(int target) Returns true if the target value exists in the recovered binary tree.

Example 1:

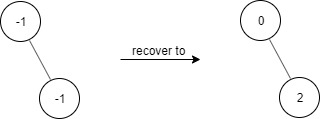
Input
["FindElements","find","find"]
[[[-1,null,-1]],[1],[2]]
Output
[null,false,true]
Explanation
FindElements findElements = new FindElements([-1,null,-1]);
findElements.find(1); // return False
findElements.find(2); // return True 

Example 2:

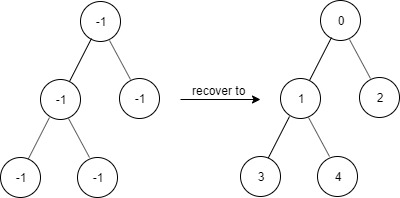
Input
["FindElements","find","find","find"]
[[[-1,-1,-1,-1,-1]],[1],[3],[5]]
Output
[null,true,true,false]
Explanation
FindElements findElements = new FindElements([-1,-1,-1,-1,-1]);
findElements.find(1); // return True
findElements.find(3); // return True
findElements.find(5); // return False

Example 3:

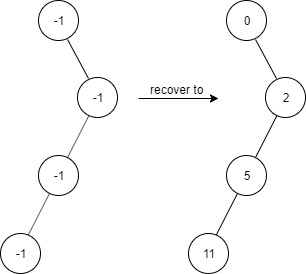
Input
["FindElements","find","find","find","find"]
[[[-1,null,-1,-1,null,-1]],[2],[3],[4],[5]]
Output
[null,true,false,false,true]
Explanation
FindElements findElements = new FindElements([-1,null,-1,-1,null,-1]);
findElements.find(2); // return True
findElements.find(3); // return False
findElements.find(4); // return False
findElements.find(5); // return True

Constraints:

• TreeNode.val == -1
• The height of the binary tree is less than or equal to 20
• The total number of nodes is between [1, 104]
• Total calls of find() is between [1, 104]
• 0 <= target <= 106

Approach 01

class FindElements {
public:
    FindElements(TreeNode* root) {
        dfs(root,0);
    }
    
    bool find(int target) {
        return result.contains(target);
    }

private:
    unordered_set<int> result;

    void dfs(TreeNode* root, int value){
        if(root==nullptr){
            return;
        }
        root->val = value;
        result.insert(value);
        dfs(root->left, value*2+1);
        dfs(root->right, value*2+2);
    }
};

class FindElements:

    def __init__(self, root: Optional[TreeNode]):
        self.result=set()
        self.dfs(root, 0)

    def find(self, target: int) -> bool:
        return target in self.result
    
    def dfs(self, root: TreeNode | None, value: int)->None:
        if(root is None):
            return
        
        root.val = value
        self.result.add(value)
        self.dfs(root.left, root.val*2+1)
        self.dfs(root.right, root.val*2+2)

Time Complexity:

• Tree Reconstruction:

  During the dfs traversal, each node is visited once, leading to a time complexity of \( O(n) \), where \( n \) is the number of nodes in the tree.

• Insertion into unordered_set:

  Each insertion operation in unordered_set takes \( O(1) \) on average, resulting in a total of \( O(n) \) for storing all nodes.

• Find Operation:

  Checking the presence of an element in unordered_set is an average \( O(1) \) operation.

• Total Time Complexity:

  The overall complexity is \( O(n) \) for construction and \( O(1) \) for each find query.

Space Complexity:

• Tree Storage:

  The unordered_set stores at most \( O(n) \) elements.

• Recursive Stack:

  In the worst case (a skewed tree), the recursion depth is \( O(n) \), leading to an additional \( O(n) \) space usage.

• Total Space Complexity:

  The overall space complexity is \( O(n) \).