129. Sum Root to Leaf Numbers

You are given the root of a binary tree containing digits from 0 to 9 only.

Each root-to-leaf path in the tree represents a number.

• For example, the root-to-leaf path 1 -> 2 -> 3 represents the number 123.

Return the total sum of all root-to-leaf numbers. Test cases are generated so that the answer will fit in a 32-bit integer.

A leaf node is a node with no children.

Example 1:

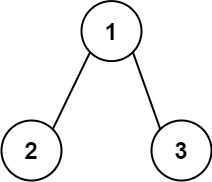
Input: root = [1,2,3]
Output: 25
Explanation:
The root-to-leaf path 1->2 represents the number 12. The root-to-leaf path 1->3 represents the number 13. Therefore, sum = 12 + 13 = 25.

Example 2:

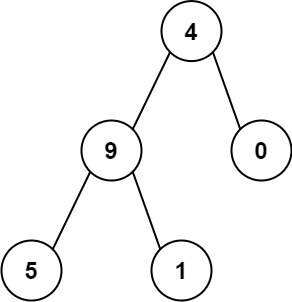
Input: root = [4,9,0,5,1]
Output: 1026
Explanation:
The root-to-leaf path 4->9->5 represents the number 495. The root-to-leaf path 4->9->1 represents the number 491. The root-to-leaf path 4->0 represents the number 40. Therefore, sum = 495 + 491 + 40 = 1026.

Constraints:

• The number of nodes in the tree is in the range [1, 1000].
• 0 <= Node.val <= 9
• The depth of the tree will not exceed 10.

Approach 01:

#include <bits/stdc++.h>

using namespace std;

struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode() : val(0), left(nullptr), right(nullptr) {}
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
    TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};

class Solution {
public:
    int solve(TreeNode* root,int current){
        if(!root){
            return 0;
        }
        current = (current*10) + root->val;
        if(root->left == NULL && root->right == NULL){
            return current; 
        }

        int left = solve(root->left, current);
        int right = solve(root->right, current);

        return (left + right);
    }
    int sumNumbers(TreeNode* root) {
        return solve(root, 0); 
    }
};

from typing import *
 
class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

class Solution:
    def solve(self, root, current):
        if(root == None):
            return 0
        current = current*10 + root.val
        if(root.left == None and root.right == None):
            return current
        left = self.solve(root.left, current)
        right = self.solve(root.right, current)
        return (left + right)
    
    def sumNumbers(self, root: Optional[TreeNode]) -> int:
        result = self.solve(root, 0)
        return result

Time Complexity

• Recursive Traversal:

  The sumNumbers function calls solve recursively on each node of the tree. Each node is visited once.

• Overall Time Complexity:

  The overall time complexity is \( O(n) \), where \( n \) is the number of nodes in the binary tree. This is because each node is visited exactly once.

Space Complexity

• Recursive Stack Space:

  The space complexity is determined by the maximum depth of the recursion stack. In the worst case, this depth is equal to the height of the tree.

• Overall Space Complexity:

  The overall space complexity is \( O(h) \), where \( h \) is the height of the binary tree. In the worst case, for a skewed tree, the space complexity can be \( O(n) \). For a balanced tree, the space complexity will be \( O(\log n) \).