There are n cities numbered from 0 to n-1. Given the array edges where edges[i] = [fromi, toi, weighti] represents a bidirectional and weighted edge between cities fromi and toi, and given the integer distanceThreshold.
Return the city with the smallest number of cities that are reachable through some path and whose distance is at most distanceThreshold, If there are multiple such cities, return the city with the greatest number.
Notice that the distance of a path connecting cities i and j is equal to the sum of the edges’ weights along that path.
Example 1:
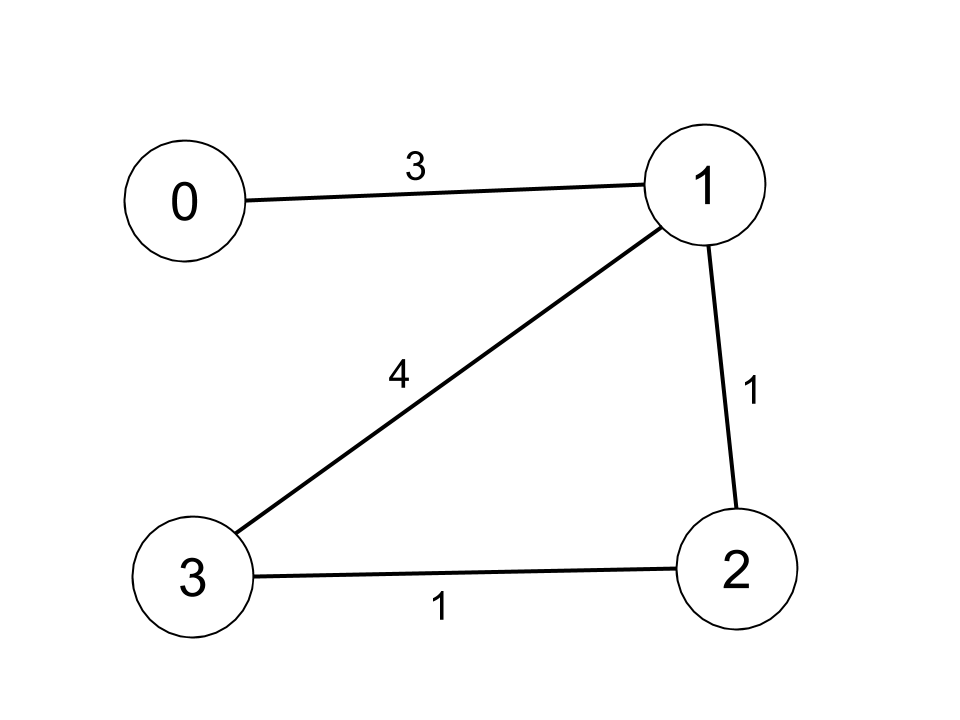
Input: n = 4, edges = [[0,1,3],[1,2,1],[1,3,4],[2,3,1]], distanceThreshold = 4 Output: 3 Explanation: The figure above describes the graph. The neighboring cities at a distanceThreshold = 4 for each city are: City 0 -> [City 1, City 2] City 1 -> [City 0, City 2, City 3] City 2 -> [City 0, City 1, City 3] City 3 -> [City 1, City 2] Cities 0 and 3 have 2 neighboring cities at a distanceThreshold = 4, but we have to return city 3 since it has the greatest number.
Example 2:
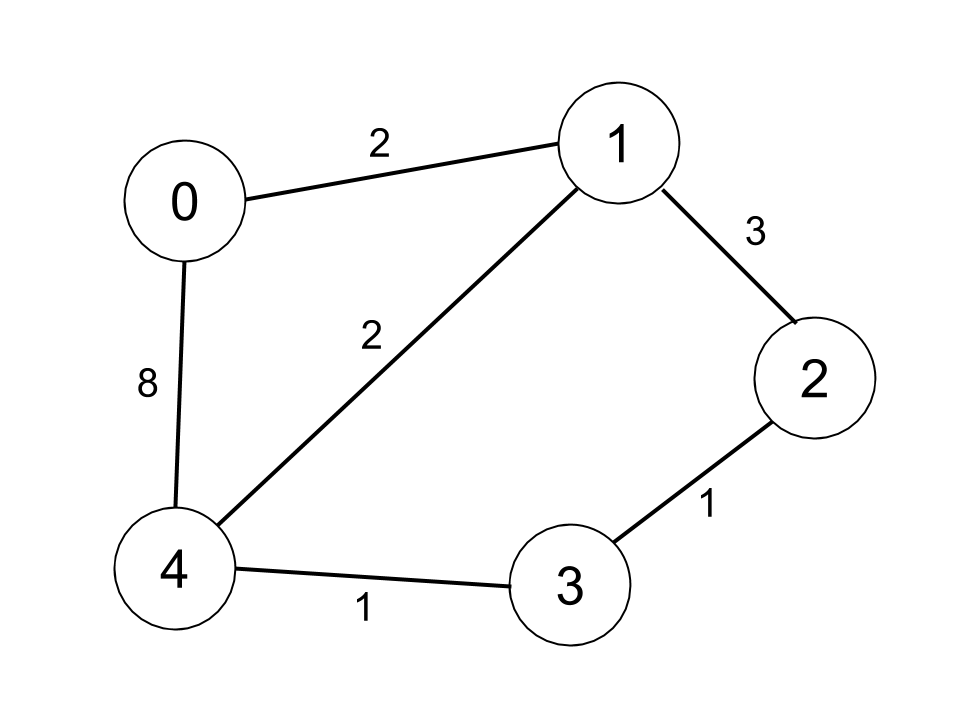
Input: n = 5, edges = [[0,1,2],[0,4,8],[1,2,3],[1,4,2],[2,3,1],[3,4,1]], distanceThreshold = 2 Output: 0 Explanation: The figure above describes the graph. The neighboring cities at a distanceThreshold = 2 for each city are: City 0 -> [City 1] City 1 -> [City 0, City 4] City 2 -> [City 3, City 4] City 3 -> [City 2, City 4] City 4 -> [City 1, City 2, City 3] The city 0 has 1 neighboring city at a distanceThreshold = 2.
Constraints:
2 <= n <= 1001 <= edges.length <= n * (n - 1) / 2edges[i].length == 30 <= fromi < toi < n1 <= weighti, distanceThreshold <= 10^4- All pairs
(fromi, toi)are distinct.
Approach 01
-
C++
-
Python
#include <vector>
#include <algorithm>
using namespace std;
class Solution {
public:
int findTheCity(int n, vector<vector<int>>& edges, int distanceThreshold) {
int resultCity = -1;
int minReachableCities = n;
const vector<vector<int>> distanceMatrix = floydWarshall(n, edges, distanceThreshold);
// Iterate through each city to find the number of reachable cities within the distance threshold
for (int currentCity = 0; currentCity < n; ++currentCity) {
int reachableCitiesCount = 0;
for (int targetCity = 0; targetCity < n; ++targetCity) {
if (distanceMatrix[currentCity][targetCity] <= distanceThreshold) {
++reachableCitiesCount;
}
}
// Update the result city if the current city has fewer or equal reachable cities
if (reachableCitiesCount <= minReachableCities) {
resultCity = currentCity;
minReachableCities = reachableCitiesCount;
}
}
return resultCity;
}
private:
vector<vector<int>> floydWarshall(int n, const vector<vector<int>>& edges, int distanceThreshold) {
vector<vector<int>> distanceMatrix(n, vector<int>(n, distanceThreshold + 1));
// Initialize the distance of each city to itself as 0
for (int i = 0; i < n; ++i) {
distanceMatrix[i][i] = 0;
}
// Set the initial distances based on the given edges
for (const vector<int>& edge : edges) {
const int fromCity = edge[0];
const int toCity = edge[1];
const int weight = edge[2];
distanceMatrix[fromCity][toCity] = weight;
distanceMatrix[toCity][fromCity] = weight;
}
// Apply Floyd-Warshall algorithm to compute the shortest paths between all pairs of cities
for (int intermediate = 0; intermediate < n; ++intermediate) {
for (int start = 0; start < n; ++start) {
for (int end = 0; end < n; ++end) {
distanceMatrix[start][end] = min(distanceMatrix[start][end], distanceMatrix[start][intermediate] + distanceMatrix[intermediate][end]);
}
}
}
return distanceMatrix;
}
};
from typing import List
class Solution:
def findTheCity(self, n: int, edges: List[List[int]], distanceThreshold: int) -> int:
resultCity = -1
minReachableCities = n
distanceMatrix = self.floydWarshall(n, edges, distanceThreshold)
# Iterate through each city to find the number of reachable cities within the distance threshold
for currentCity in range(n):
reachableCitiesCount = 0
for targetCity in range(n):
if distanceMatrix[currentCity][targetCity] <= distanceThreshold:
reachableCitiesCount += 1
# Update the result city if the current city has fewer or equal reachable cities
if reachableCitiesCount <= minReachableCities:
resultCity = currentCity
minReachableCities = reachableCitiesCount
return resultCity
def floydWarshall(self, n: int, edges: List[List[int]], distanceThreshold: int) -> List[List[int]]:
distanceMatrix = [[distanceThreshold + 1] * n for _ in range(n)]
# Initialize the distance of each city to itself as 0
for i in range(n):
distanceMatrix[i][i] = 0
# Set the initial distances based on the given edges
for edge in edges:
fromCity, toCity, weight = edge
distanceMatrix[fromCity][toCity] = weight
distanceMatrix[toCity][fromCity] = weight
# Apply Floyd-Warshall algorithm to compute the shortest paths between all pairs of cities
for intermediate in range(n):
for start in range(n):
for end in range(n):
distanceMatrix[start][end] = min(distanceMatrix[start][end], distanceMatrix[start][intermediate] + distanceMatrix[intermediate][end])
return distanceMatrix
Time Complexity
- Floyd-Warshall Algorithm:
Floyd-Warshall algorithm involves three nested loops, each iterating over the number of cities
n. Therefore, the time complexity is \( O(n^3) \). - Counting Reachable Cities:
Iterating through each city to count the number of reachable cities involves two nested loops, each iterating over
n. This takes \( O(n^2) \) time. - Overall Time Complexity:
The overall time complexity is dominated by the Floyd-Warshall algorithm, making it \( O(n^3) \).
Space Complexity
- Distance Matrix:
The distance matrix is a 2D vector of size
n x n, which takes \( O(n^2) \) space. - Other Variables:
Other variables such as
resultCity,minReachableCities, and the counts used for iteration take \( O(1) \) space. - Overall Space Complexity:
The overall space complexity is \( O(n^2) \) due to the distance matrix.