1368. Minimum Cost to Make at Least One Valid Path in a Grid

Given an m x n grid. Each cell of the grid has a sign pointing to the next cell you should visit if you are currently in this cell. The sign of grid[i][j] can be:

• 1 which means go to the cell to the right. (i.e go from grid[i][j] to grid[i][j + 1])
• 2 which means go to the cell to the left. (i.e go from grid[i][j] to grid[i][j - 1])
• 3 which means go to the lower cell. (i.e go from grid[i][j] to grid[i + 1][j])
• 4 which means go to the upper cell. (i.e go from grid[i][j] to grid[i - 1][j])

Notice that there could be some signs on the cells of the grid that point outside the grid.

You will initially start at the upper left cell (0, 0). A valid path in the grid is a path that starts from the upper left cell (0, 0) and ends at the bottom-right cell (m - 1, n - 1) following the signs on the grid. The valid path does not have to be the shortest.

You can modify the sign on a cell with cost = 1. You can modify the sign on a cell one time only.

Return the minimum cost to make the grid have at least one valid path.

Example 1:

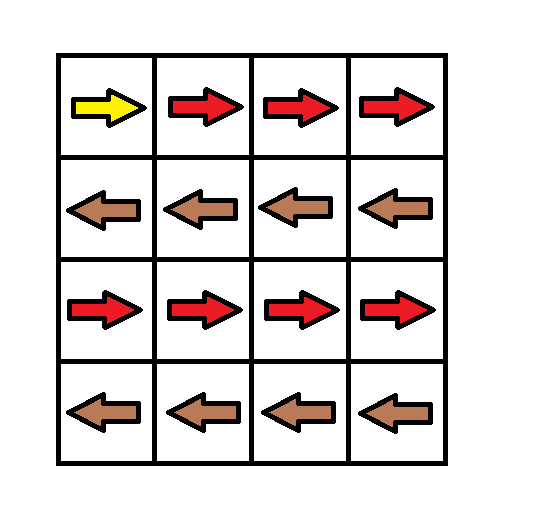
Input: grid = [[1,1,1,1],[2,2,2,2],[1,1,1,1],[2,2,2,2]]
Output: 3
Explanation: You will start at point (0, 0).
The path to (3, 3) is as follows. (0, 0) --> (0, 1) --> (0, 2) --> (0, 3) change the arrow to down with cost = 1 --> (1, 3) --> (1, 2) --> (1, 1) --> (1, 0) change the arrow to down with cost = 1 --> (2, 0) --> (2, 1) --> (2, 2) --> (2, 3) change the arrow to down with cost = 1 --> (3, 3)
The total cost = 3.

Example 2:

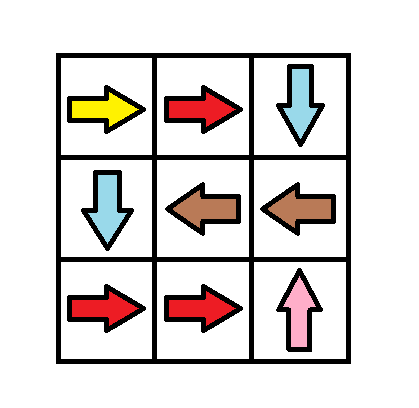
Input: grid = [[1,1,3],[3,2,2],[1,1,4]]
Output: 0
Explanation: You can follow the path from (0, 0) to (2, 2).

Example 3:

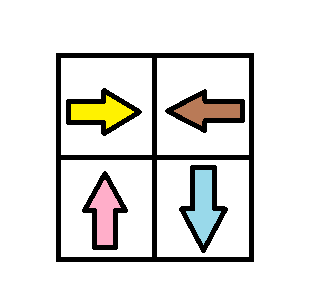
Input: grid = [[1,2],[4,3]]
Output: 1

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 100
• 1 <= grid[i][j] <= 4

Approach 01:

#include <vector>
#include <queue>
#include <utility>

class Solution {
 public:
  int minCost(std::vector<std::vector<int>>& grid) {
    const int rows = grid.size();
    const int cols = grid[0].size();
    std::vector<std::vector<int>> costMemo(rows, std::vector<int>(cols, -1));
    std::queue<std::pair<int, int>> bfsQueue;

    // Start DFS from the top-left corner with an initial cost of 0
    dfs(grid, 0, 0, 0, bfsQueue, costMemo);

    // Process the BFS queue to explore all possible paths
    for (int currentCost = 1; !bfsQueue.empty(); ++currentCost) {
      for (int size = bfsQueue.size(); size > 0; --size) {
        const auto [currentRow, currentCol] = bfsQueue.front();
        bfsQueue.pop();
        for (const auto& [dx, dy] : directions)
          dfs(grid, currentRow + dx, currentCol + dy, currentCost, bfsQueue, costMemo);
      }
    }

    // Return the minimum cost to reach the bottom-right corner
    return costMemo.back().back();
  }

 private:
  // Directions: right, left, down, up
  static constexpr int directions[4][2] = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};

  void dfs(const std::vector<std::vector<int>>& grid, int row, int col, int currentCost,
           std::queue<std::pair<int, int>>& bfsQueue, std::vector<std::vector<int>>& costMemo) {
    // Check for out-of-bounds indices
    if (row < 0 || row >= grid.size() || col < 0 || col >= grid[0].size())
      return;
    // If this cell has already been visited with a lower cost, skip it
    if (costMemo[row][col] != -1)
      return;

    // Mark the current cell with the current cost
    costMemo[row][col] = currentCost;
    // Add the current cell to the BFS queue
    bfsQueue.emplace(row, col);

    // Move in the direction indicated by the current cell's value
    const auto& [dx, dy] = directions[grid[row][col] - 1];
    dfs(grid, row + dx, col + dy, currentCost, bfsQueue, costMemo);
  }
};

from typing import List
from collections import deque

class Solution:
    def minCost(self, grid: List[List[int]]) -> int:
        rows = len(grid)
        cols = len(grid[0])
        costMemo = [[-1] * cols for _ in range(rows)]
        bfsQueue = deque()

        # Start DFS from the top-left corner with an initial cost of 0
        self.dfs(grid, 0, 0, 0, bfsQueue, costMemo)

        # Process the BFS queue to explore all possible paths
        currentCost = 1
        while bfsQueue:
            for _ in range(len(bfsQueue)):
                currentRow, currentCol = bfsQueue.popleft()
                for dx, dy in self.directions:
                    self.dfs(grid, currentRow + dx, currentCol + dy, currentCost, bfsQueue, costMemo)
            currentCost += 1

        # Return the minimum cost to reach the bottom-right corner
        return costMemo[-1][-1]

    # Directions: right, left, down, up
    directions = [(0, 1), (0, -1), (1, 0), (-1, 0)]

    def dfs(self, grid: List[List[int]], row: int, col: int, currentCost: int,
            bfsQueue: deque, costMemo: List[List[int]]) -> None:
        # Check for out-of-bounds indices
        if not (0 <= row < len(grid)) or not (0 <= col < len(grid[0])):
            return
        # If this cell has already been visited with a lower cost, skip it
        if costMemo[row][col] != -1:
            return

        # Mark the current cell with the current cost
        costMemo[row][col] = currentCost
        # Add the current cell to the BFS queue
        bfsQueue.append((row, col))

        # Move in the direction indicated by the current cell's value
        dx, dy = self.directions[grid[row][col] - 1]
        self.dfs(grid, row + dx, col + dy, currentCost, bfsQueue, costMemo)

Time Complexity:

• DFS Traversal:

  The dfs function visits each cell of the grid exactly once and marks it with a cost. Since there are \( m \times n \) cells in the grid, the DFS traversal takes \( O(m \times n) \).

• BFS Traversal:

  The BFS processes all cells in the grid, and each cell is added to the queue at most once. Thus, the BFS traversal also takes \( O(m \times n) \).

• Overall Time Complexity:

  The overall time complexity is \( O(m \times n) \).

Space Complexity:

• Cost Memoization Array:

  A 2D array costMemo of size \( m \times n \) is used to store the minimum cost for each cell, requiring \( O(m \times n) \) space.

• BFS Queue:

  The BFS queue can hold up to \( O(m \times n) \) elements in the worst case, which contributes \( O(m \times n) \) to the space complexity.

• Overall Space Complexity:

  The overall space complexity is \( O(m \times n) \).