1382. Balance a Binary Search Tree

Given the root of a binary search tree, return a balanced binary search tree with the same node values. If there is more than one answer, return any of them.

A binary search tree is balanced if the depth of the two subtrees of every node never differs by more than 1.

Example 1:

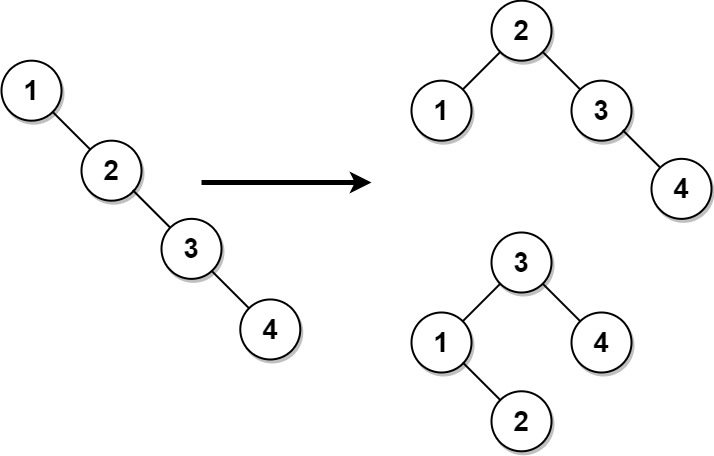
Input: root = [1,null,2,null,3,null,4,null,null]
Output: [2,1,3,null,null,null,4]
Explanation: This is not the only correct answer, [3,1,4,null,2] is also correct.

Example 2:

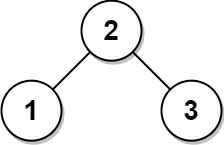
Input: root = [2,1,3]
Output: [2,1,3]

Constraints:

• The number of nodes in the tree is in the range [1, 104].
• 1 <= Node.val <= 105

Approach 01:

#include <vector>

using namespace std;

struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode() : val(0), left(nullptr), right(nullptr) {}
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
    TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};

class Solution {
public:
    TreeNode* balanceBST(TreeNode* root) {
        vector<int> nums;
        inorderTraversal(root, nums);
        return buildBalancedBST(nums, 0, nums.size() - 1);
    }

private:
    void inorderTraversal(TreeNode* root, vector<int>& nums) {
        if (root == nullptr)
            return;
        inorderTraversal(root->left, nums);
        nums.push_back(root->val);
        inorderTraversal(root->right, nums);
    }

    TreeNode* buildBalancedBST(const vector<int>& nums, int left, int right) {
        if (left > right)
            return nullptr;
        int mid = (left + right) / 2;
        TreeNode* root = new TreeNode(nums[mid]);
        root->left = buildBalancedBST(nums, left, mid - 1);
        root->right = buildBalancedBST(nums, mid + 1, right);
        return root;
    }
};

from typing import List, Optional

class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

class Solution:
    def balanceBST(self, root: TreeNode) -> TreeNode:
        nums = []
        self.inorder_traversal(root, nums)
        return self.build_balanced_bst(nums, 0, len(nums) - 1)

    def inorder_traversal(self, root: Optional[TreeNode], nums: List[int]) -> None:
        if root is None:
            return
        self.inorder_traversal(root.left, nums)
        nums.append(root.val)
        self.inorder_traversal(root.right, nums)

    def build_balanced_bst(self, nums: List[int], left: int, right: int) -> Optional[TreeNode]:
        if left > right:
            return None
        mid = (left + right) // 2
        root = TreeNode(nums[mid])
        root.left = self.build_balanced_bst(nums, left, mid - 1)
        root.right = self.build_balanced_bst(nums, mid + 1, right)
        return root

Time Complexity:

• Inorder Traversal:

  The inorderTraversal function visits each node exactly once.

  This takes \( O(n) \) time, where \( n \) is the number of nodes in the tree.

• Building the Balanced BST:

  The buildBalancedBST function constructs the balanced BST from the sorted list.

  This is a recursive function that divides the list into two halves at each step.

  Each level of recursion processes all \( n \) elements once.

  Therefore, the time complexity for this function is \( O(n) \).

• Overall Time Complexity:

  The total time complexity of the balanceBST function is \( O(n) \) + \( O(n) \) = \( O(n) \).

Space Complexity:

• Inorder Traversal:

  The space required for the nums vector to store the inorder traversal is \( O(n) \).

  The recursion stack space for the inorder traversal function is \( O(h) \), where \( h \) is the height of the tree.

  In the worst case, the height \( h \) can be \( O(n) \) (for a skewed tree).

  In the best case (balanced tree), the height \( h \) is \( O(\log n) \).

• Building the Balanced BST:

  The space required for the recursion stack during the construction of the balanced BST is also \( O(h) \).

  As with the inorder traversal, this can be \( O(n) \) in the worst case and \( O(\log n) \) in the best case.

• Overall Space Complexity:

  The space complexity is dominated by the space required to store the inorder traversal, which is \( O(n) \), plus the recursion stack space, which is \( O(h) \).

  Hence, the total space complexity is \( O(n) \).