1518. Water Bottles

There are numBottles water bottles that are initially full of water. You can exchange numExchange empty water bottles from the market with one full water bottle.

The operation of drinking a full water bottle turns it into an empty bottle.

Given the two integers numBottles and numExchange, return the maximum number of water bottles you can drink.

Example 1:

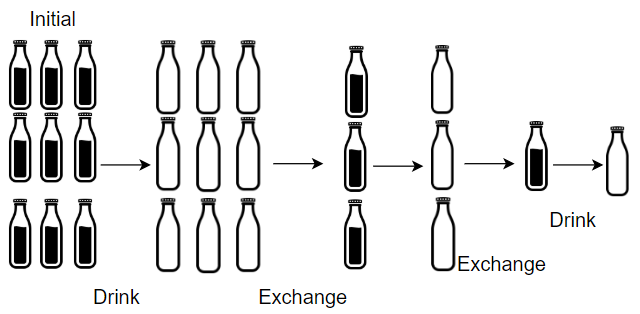
Input: numBottles = 9, numExchange = 3
Output: 13
Explanation: You can exchange 3 empty bottles to get 1 full water bottle.
Number of water bottles you can drink: 9 + 3 + 1 = 13.

Example 2:

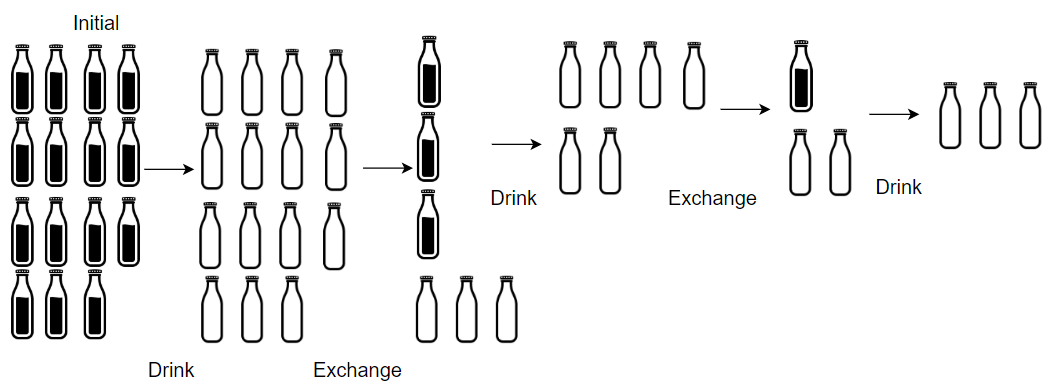
Input: numBottles = 15, numExchange = 4
Output: 19
Explanation: You can exchange 4 empty bottles to get 1 full water bottle. 
Number of water bottles you can drink: 15 + 3 + 1 = 19.

Constraints:

• 1 <= numBottles <= 100
• 2 <= numExchange <= 100

Approach 01:

class Solution {
public:
    int numWaterBottles(int numBottles, int numExchange) {
        return numBottles + (numBottles - 1) / (numExchange - 1);
    }
};

from typing import *

class Solution:
    def numWaterBottles(self, numBottles: int, numExchange: int) -> int:
        return numBottles + (numBottles - 1) // (numExchange - 1)

Time Complexity

• Arithmetic Operations:

  Calculating the result involves basic arithmetic operations which take \( O(1) \) time.

• Overall Time Complexity:

  The overall time complexity is \( O(1) \) as all operations are constant time.

Space Complexity

• Space Usage:

  The algorithm uses a constant amount of space for variables `numBottles` and `numExchange`, which takes \( O(1) \) space.

• Overall Space Complexity:

  The overall space complexity is \( O(1) \) as no additional data structures are used.

Approach 02:

#include <bits/stdc++.h>

using namespace std;

class Solution {
public:
    int numWaterBottles(int numBottles, int numExchange) {
        int result = numBottles;

        while (numBottles >= numExchange) {
            result += numBottles / numExchange;
            numBottles = numBottles / numExchange + numBottles % numExchange;
        }

        return result;
    }
};

from typing import *

class Solution:
    def numWaterBottles(self, numBottles: int, numExchange: int) -> int:
        result = numBottles

        while numBottles >= numExchange:
            result += numBottles // numExchange
            numBottles = numBottles // numExchange + numBottles % numExchange

        return result

Time Complexity

• Initialization:

  Initializing `result` takes \( O(1) \) time.

• While Loop:

  The while loop runs as long as `numBottles` is greater than or equal to `numExchange`. In each iteration, the number of bottles decreases by at least 1. Hence, the number of iterations is at most proportional to `numBottles`, resulting in \( O(\log_{numExchange}(numBottles)) \) time complexity.

• Overall Time Complexity:

  The overall time complexity is \( O(\log_{numExchange}(numBottles)) \).

Space Complexity

• Space Usage:

  The algorithm uses a constant amount of extra space for variables `result` and `numBottles`, which takes \( O(1) \) space.

• Overall Space Complexity:

  The overall space complexity is \( O(1) \) as there are no additional data structures used that grow with input size.