1530. Number of Good Leaf Nodes Pairs

You are given the root of a binary tree and an integer distance. A pair of two different leaf nodes of a binary tree is said to be good if the length of the shortest path between them is less than or equal to distance.

Return the number of good leaf node pairs in the tree.

Example 1:

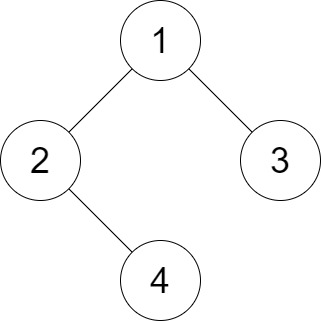
Input: root = [1,2,3,null,4], distance = 3
Output: 1
Explanation: The leaf nodes of the tree are 3 and 4 and the length of the shortest path between them is 3. This is the only good pair.

Example 2:

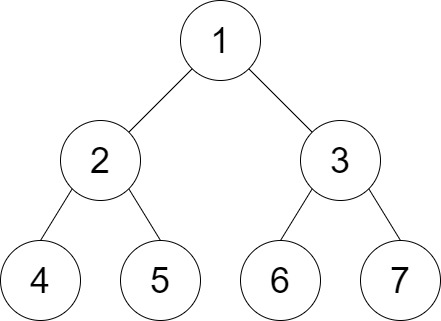
Input: root = [1,2,3,4,5,6,7], distance = 3
Output: 2
Explanation: The good pairs are [4,5] and [6,7] with shortest path = 2. The pair [4,6] is not good because the length of ther shortest path between them is 4.

Example 3:

Input: root = [7,1,4,6,null,5,3,null,null,null,null,null,2], distance = 3
Output: 1
Explanation: The only good pair is [2,5].

Constraints:

• The number of nodes in the tree is in the range [1, 210].
• 1 <= Node.val <= 100
• 1 <= distance <= 10

Approach01:

#include <bits/stdc++.h>

using namespace std;

class Solution {
public:
    int countPairs(TreeNode* root, int distance) {
        int pairCount = 0;
        dfs(root, distance, pairCount);
        return pairCount;
    }

private:
    vector<int> dfs(TreeNode* root, int maxDistance, int& pairCount) {
        vector<int> distances(maxDistance + 1);  // {distance: the number of leaf nodes}
        if (root == nullptr)
            return distances;
        if (root->left == nullptr && root->right == nullptr) {
            distances[0] = 1;
            return distances;
        }

        const vector<int> leftDistances = dfs(root->left, maxDistance, pairCount);
        const vector<int> rightDistances = dfs(root->right, maxDistance, pairCount);

        for (int leftDist = 0; leftDist < maxDistance; ++leftDist)
            for (int rightDist = 0; rightDist < maxDistance; ++rightDist)
                if (leftDist + rightDist + 2 <= maxDistance)
                    pairCount += leftDistances[leftDist] * rightDistances[rightDist];

        for (int dist = 0; dist < maxDistance; ++dist)
            distances[dist + 1] = leftDistances[dist] + rightDistances[dist];

        return distances;
    }
};

from typing import *

class Solution:
    def countPairs(self, root: TreeNode, distance: int) -> int:
        self.pairCount = 0
        self.dfs(root, distance)
        return self.pairCount

    def dfs(self, root: TreeNode, maxDistance: int) -> List[int]:
        distances = [0] * (maxDistance + 1)  # {distance: the number of leaf nodes}
        if root is None:
            return distances
        if root.left is None and root.right is None:
            distances[0] = 1
            return distances

        leftDistances = self.dfs(root.left, maxDistance)
        rightDistances = self.dfs(root.right, maxDistance)

        for leftDist in range(maxDistance):
            for rightDist in range(maxDistance):
                if leftDist + rightDist + 2 <= maxDistance:
                    self.pairCount += leftDistances[leftDist] * rightDistances[rightDist]

        for dist in range(maxDistance):
            distances[dist + 1] = leftDistances[dist] + rightDistances[dist]

        return distances

Time Complexity

• Traversal:

  The algorithm performs a Depth-First Search (DFS) traversal of the tree, visiting each node exactly once. Thus, the time complexity for traversal is \( O(n) \), where \( n \) is the number of nodes in the tree.

• Distance Calculation:

  For each node, the algorithm iterates through the distances array with a maximum length of maxDistance + 1. Since this array length is a constant relative to the number of nodes, the time complexity remains \( O(n) \).

• Overall Time Complexity:

  The overall time complexity is \( O(n) \).

Space Complexity

• Auxiliary Space for Distances Array:

  The distances array has a size of maxDistance + 1 at each node. Since this is a constant relative to the number of nodes, it contributes \( O(1) \) to the space complexity at each node.

• Recursive Call Stack:

  The depth of the recursion stack can go up to the height of the tree. In the worst case, the height of the tree can be \( O(n) \), resulting in a space complexity of \( O(n) \) for the call stack.

• Overall Space Complexity:

  The overall space complexity is \( O(n) \) due to the recursive call stack.