You are given an m x n binary grid grid where 1 represents land and 0 represents water. An island is a maximal 4-directionally (horizontal or vertical) connected group of 1‘s.
The grid is said to be connected if we have exactly one island, otherwise is said disconnected.
In one day, we are allowed to change any single land cell (1) into a water cell (0).
Return the minimum number of days to disconnect the grid.
Example 1:
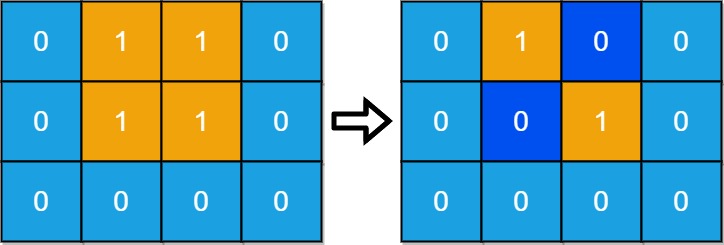
Input: grid = [[0,1,1,0],[0,1,1,0],[0,0,0,0]] Output: 2 Explanation: We need at least 2 days to get a disconnected grid. Change land grid[1][1] and grid[0][2] to water and get 2 disconnected island.
Example 2:

Input: grid = [[1,1]] Output: 2 Explanation: Grid of full water is also disconnected ([[1,1]] -> [[0,0]]), 0 islands.
Constraints:
m == grid.lengthn == grid[i].length1 <= m, n <= 30grid[i][j]is either0or1.
Approach 01:
-
C++
-
Python
#include <vector>
#include <algorithm>
using namespace std;
class Solution {
public:
// Direction vector for traversing the grid in four directions (up, right, down, left).
const vector<int> directions = {-1, 0, 1, 0, -1};
// Variables to store the number of rows and columns in the grid.
int numRows, numCols;
// Function to determine the minimum number of days required to disconnect the grid.
int minDays(vector<vector<int>>& grid) {
// Initialize grid dimensions.
numRows = grid.size();
numCols = grid[0].size();
// Check if the grid is already disconnected or completely connected.
if (countIslands(grid) != 1) {
return 0; // No day required if the grid is already disconnected.
}
// Try removing each land cell to see if it isolates the grid.
for (int row = 0; row < numRows; ++row) {
for (int col = 0; col < numCols; ++col) {
if (grid[row][col] == 1) { // Check if the current cell is land.
grid[row][col] = 0; // Temporarily remove the land cell.
if (countIslands(grid) != 1) {
return 1; // If removing the cell disconnects the grid, return 1 day.
}
grid[row][col] = 1; // Restore the land cell.
}
}
}
// If no single removal disconnects the grid, return 2 days as the required time.
return 2;
}
private:
// Helper function to count the number of islands (connected land components) in the grid.
int countIslands(vector<vector<int>>& grid) {
int islandCount = 0;
// Traverse the grid to identify islands.
for (int row = 0; row < numRows; ++row) {
for (int col = 0; col < numCols; ++col) {
if (grid[row][col] == 1) { // Start DFS if a land cell is found.
dfs(row, col, grid);
++islandCount; // Increment the island count after completing DFS.
}
}
}
// Reset the grid to its original state after counting.
for (int row = 0; row < numRows; ++row) {
for (int col = 0; col < numCols; ++col) {
if (grid[row][col] == 2) {
grid[row][col] = 1; // Restore the state from temporary 2 to land (1).
}
}
}
return islandCount; // Return the total number of islands.
}
// Depth-first search (DFS) to mark all cells of a connected component.
void dfs(int row, int col, vector<vector<int>>& grid) {
grid[row][col] = 2; // Temporarily mark the cell to avoid revisiting.
// Explore all four adjacent directions.
for (int dir = 0; dir < 4; ++dir) {
int newRow = row + directions[dir], newCol = col + directions[dir + 1];
// Continue DFS if the adjacent cell is within bounds and is land.
if (newRow >= 0 && newRow < numRows && newCol >= 0 && newCol < numCols && grid[newRow][newCol] == 1) {
dfs(newRow, newCol, grid);
}
}
}
};
from typing import List
class Solution:
# Direction array to facilitate grid traversal.
directions = [-1, 0, 1, 0, -1]
# Function to determine the minimum number of days required to disconnect the grid.
def minDays(self, grid: List[List[int]]) -> int:
# Initialize grid dimensions.
self.numRows = len(grid)
self.numCols = len(grid[0])
# Check if the grid is already disconnected or completely connected.
if self.countIslands(grid) != 1:
return 0 # No day required if the grid is already disconnected.
# Try removing each land cell to see if it isolates the grid.
for row in range(self.numRows):
for col in range(self.numCols):
if grid[row][col] == 1: # Check if the current cell is land.
grid[row][col] = 0 # Temporarily remove the land cell.
if self.countIslands(grid) != 1:
return 1 # If removing the cell disconnects the grid, return 1 day.
grid[row][col] = 1 # Restore the land cell.
# If no single removal disconnects the grid, return 2 days as the required time.
return 2
# Helper function to count the number of islands (connected land components) in the grid.
def countIslands(self, grid: List[List[int]]) -> int:
islandCount = 0
# Traverse the grid to identify islands.
for row in range(self.numRows):
for col in range(self.numCols):
if grid[row][col] == 1: # Start DFS if a land cell is found.
self.dfs(row, col, grid)
islandCount += 1 # Increment the island count after completing DFS.
# Reset the grid to its original state after counting.
for row in range(self.numRows):
for col in range(self.numCols):
if grid[row][col] == 2:
grid[row][col] = 1 # Restore the state from temporary 2 to land (1).
return islandCount # Return the total number of islands.
# Depth-first search (DFS) to mark all cells of a connected component.
def dfs(self, row: int, col: int, grid: List[List[int]]) -> None:
grid[row][col] = 2 # Temporarily mark the cell to avoid revisiting.
# Explore all four adjacent directions.
for dir in range(4):
newRow = row + self.directions[dir]
newCol = col + self.directions[dir + 1]
# Continue DFS if the adjacent cell is within bounds and is land.
if 0 <= newRow < self.numRows and 0 <= newCol < self.numCols and grid[newRow][newCol] == 1:
self.dfs(newRow, newCol, grid)
Time Complexity
- Counting Islands:
The `countIslands` function uses Depth-First Search (DFS) to traverse the grid. In the worst case, it visits every cell in the grid, leading to a time complexity of \( O(R \times C) \), where \( R \) is the number of rows and \( C \) is the number of columns.
- Checking Each Cell:
In the main
minDaysfunction, the algorithm iterates over all cells in the grid and callscountIslandsafter temporarily removing a land cell. The time complexity for this is \( O(R \times C) \) iterations, and for each iteration, it callscountIslands, which takes \( O(R \times C) \) time. Therefore, the total time complexity is \( O((R \times C) \times (R \times C)) = O(R^2 \times C^2) \). - Overall Time Complexity:
The overall time complexity is dominated by the nested loop and island counting, resulting in \( O(R^2 \times C^2) \).
Space Complexity
- DFS Recursive Stack:
The space complexity of the DFS algorithm depends on the recursion stack, which in the worst case could be as deep as the number of cells in the grid, i.e., \( O(R \times C) \). However, this space is temporary and gets released after the DFS completes.
- Auxiliary Space:
The grid itself does not require extra space as it is modified in place. Therefore, the auxiliary space used by the algorithm is \( O(1) \).
- Overall Space Complexity:
The overall space complexity is \( O(R \times C) \), dominated by the DFS recursion stack.