1579. Remove Max Number of Edges to Keep Graph Fully Traversable

Alice and Bob have an undirected graph of n nodes and three types of edges:

• Type 1: Can be traversed by Alice only.
• Type 2: Can be traversed by Bob only.
• Type 3: Can be traversed by both Alice and Bob.

Given an array edges where edges[i] = [typei, ui, vi] represents a bidirectional edge of type typei between nodes ui and vi, find the maximum number of edges you can remove so that after removing the edges, the graph can still be fully traversed by both Alice and Bob. The graph is fully traversed by Alice and Bob if starting from any node, they can reach all other nodes.

Return the maximum number of edges you can remove, or return -1 if Alice and Bob cannot fully traverse the graph.

Example 1:

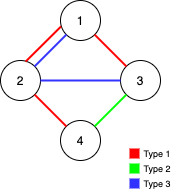
Input: n = 4, edges = [[3,1,2],[3,2,3],[1,1,3],[1,2,4],[1,1,2],[2,3,4]]
Output: 2
Explanation: If we remove the 2 edges [1,1,2] and [1,1,3]. The graph will still be fully traversable by Alice and Bob. Removing any additional edge will not make it so. So the maximum number of edges we can remove is 2.

Example 2:

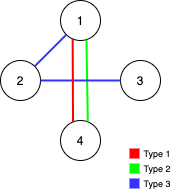
Input: n = 4, edges = [[3,1,2],[3,2,3],[1,1,4],[2,1,4]]
Output: 0
Explanation: Notice that removing any edge will not make the graph fully traversable by Alice and Bob.

Example 3:

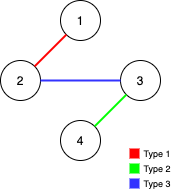
Input: n = 4, edges = [[3,2,3],[1,1,2],[2,3,4]]
Output: -1
Explanation: In the current graph, Alice cannot reach node 4 from the other nodes. Likewise, Bob cannot reach 1. Therefore it's impossible to make the graph fully traversable.

Constraints:

• 1 <= n <= 105
• 1 <= edges.length <= min(105, 3 * n * (n - 1) / 2)
• edges[i].length == 3
• 1 <= typei <= 3
• 1 <= ui < vi <= n
• All tuples (typei, ui, vi) are distinct.

Approach 01:

class UnionFind {
public:
    UnionFind(int n) : count(n), id(n), rank(n) {
        iota(id.begin(), id.end(), 0);
    }

    bool union_by_rank(int u, int v) {
        const int root_u = find(u);
        const int root_v = find(v);
        if (root_u == root_v)
            return false;
        if (rank[root_u] < rank[root_v]) {
            id[root_u] = root_v;
        } else if (rank[root_u] > rank[root_v]) {
            id[root_v] = root_u;
        } else {
            id[root_u] = root_v;
            ++rank[root_v];
        }
        --count;
        return true;
    }

    int get_count() const { return count; }

private:
    int count;
    vector<int> id;
    vector<int> rank;

    int find(int u) { return id[u] == u ? u : id[u] = find(id[u]); }
};

class Solution {
public:
    int maxNumEdgesToRemove(int n, vector<vector<int>>& edges) {
        UnionFind alice(n);
        UnionFind bob(n);
        int required_edges = 0;

        // Greedily put type 3 edges in the front.
        sort(edges.begin(), edges.end(),
             [](const vector<int>& a, const vector<int>& b) {
                 return a[0] > b[0];
             });

        for (const vector<int>& edge : edges) {
            const int type = edge[0];
            const int u = edge[1] - 1;
            const int v = edge[2] - 1;
            switch (type) {
            case 3: // Can be traversed by Alice and Bob.
                if (alice.union_by_rank(u, v) | bob.union_by_rank(u, v))
                    ++required_edges;
                break;
            case 2: // Can be traversed by Bob.
                if (bob.union_by_rank(u, v))
                    ++required_edges;
                break; // Added break statement here
            case 1:    // Can be traversed by Alice.
                if (alice.union_by_rank(u, v))
                    ++required_edges;
                break; // Added break statement here
            }
        }

        return alice.get_count() == 1 && bob.get_count() == 1 ? edges.size() - required_edges : -1;
    }
};

class UnionFind:
    def __init__(self, n):
        self.count = n
        self.id = list(range(n))
        self.rank = [0] * n

    def union_by_rank(self, u, v):
        root_u = self.find(u)
        root_v = self.find(v)
        if root_u == root_v:
            return False
        if self.rank[root_u] < self.rank[root_v]:
            self.id[root_u] = root_v
        elif self.rank[root_u] > self.rank[root_v]:
            self.id[root_v] = root_u
        else:
            self.id[root_u] = root_v
            self.rank[root_v] += 1
        self.count -= 1
        return True

    def get_count(self):
        return self.count

    def find(self, u):
        if self.id[u] != u:
            self.id[u] = self.find(self.id[u])  # Path compression
        return self.id[u]


class Solution:
    def maxNumEdgesToRemove(self, n, edges):
        alice = UnionFind(n)
        bob = UnionFind(n)
        required_edges = 0

        # Greedily put type 3 edges in the front.
        edges.sort(key=lambda x: -x[0])

        for edge in edges:
            type = edge[0]
            u = edge[1] - 1
            v = edge[2] - 1
            if type == 3:  # Can be traversed by Alice and Bob.
                if alice.union_by_rank(u, v) | bob.union_by_rank(u, v):
                    required_edges += 1
            elif type == 2:  # Can be traversed by Bob.
                if bob.union_by_rank(u, v):
                    required_edges += 1
            elif type == 1:  # Can be traversed by Alice.
                if alice.union_by_rank(u, v):
                    required_edges += 1

        return len(edges) - required_edges if alice.get_count() == 1 and bob.get_count() == 1 else -1

Time Complexity

• Initialization of UnionFind Objects: Initializing alice and bob takes \( O(n) \) time each.

• Sorting the Edges: Sorting edges takes \( O(E \log E) \) time, where E is the number of edges.

• Processing Each Edge: Iterating through each edge and performing union-find operations takes \( O(E \alpha(n)) \) time.

• Overall Time Complexity: \( O(n) + O(E \log E) + O(E \alpha(n)) \approx O(E \log E) \)

Space Complexity

• UnionFind Objects: Each UnionFind object uses \( O(n) \) space, and we have two such objects, so total space is \( O(n) \).

• Edges Vector:The edges vector uses \( O(E) \) space.

• Overall Space Complexity: \( O(n + E) \)