1765. Map of Highest Peak

You are given an integer matrix isWater of size m x n that represents a map of land and water cells.

• If isWater[i][j] == 0, cell (i, j) is a land cell.
• If isWater[i][j] == 1, cell (i, j) is a water cell.

You must assign each cell a height in a way that follows these rules:

• The height of each cell must be non-negative.
• If the cell is a water cell, its height must be 0.
• Any two adjacent cells must have an absolute height difference of at most 1. A cell is adjacent to another cell if the former is directly north, east, south, or west of the latter (i.e., their sides are touching).

Find an assignment of heights such that the maximum height in the matrix is maximized.

Return an integer matrix height of size m x n where height[i][j] is cell (i, j)‘s height. If there are multiple solutions, return any of them.

Example 1:

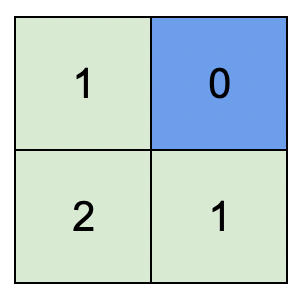
Input: isWater = [[0,1],[0,0]]
Output: [[1,0],[2,1]]
Explanation: The image shows the assigned heights of each cell.
The blue cell is the water cell, and the green cells are the land cells.

Example 2:

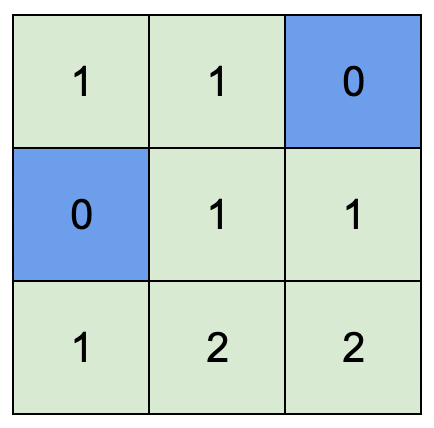
Input: isWater = [[0,0,1],[1,0,0],[0,0,0]]
Output: [[1,1,0],[0,1,1],[1,2,2]]
Explanation: A height of 2 is the maximum possible height of any assignment.
Any height assignment that has a maximum height of 2 while still meeting the rules will also be accepted.

Constraints:

• m == isWater.length
• n == isWater[i].length
• 1 <= m, n <= 1000
• isWater[i][j] is 0 or 1.
• There is at least one water cell.

Approach 01:

class Solution {
 public:
  vector<vector<int>> highestPeak(vector<vector<int>>& isWater) {
    constexpr int directions[4][2] = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
    const int rows = isWater.size();
    const int cols = isWater[0].size();
    vector<vector<int>> heights(rows, vector<int>(cols, -1));
    queue<pair<int, int>> cellsToProcess;

    // Initialize queue with all water cells and set their height to 0
    for (int row = 0; row < rows; ++row) {
      for (int col = 0; col < cols; ++col) {
        if (isWater[row][col] == 1) {
          cellsToProcess.emplace(row, col);
          heights[row][col] = 0;
        }
      }
    }

    // Perform BFS to calculate the height of each land cell
    while (!cellsToProcess.empty()) {
      const auto [currentRow, currentCol] = cellsToProcess.front();
      cellsToProcess.pop();

      for (const auto& [dx, dy] : directions) {
        const int newRow = currentRow + dx;
        const int newCol = currentCol + dy;

        // Skip invalid or already-processed cells
        if (newRow < 0 || newRow >= rows || newCol < 0 || newCol >= cols)
          continue;
        if (heights[newRow][newCol] != -1)
          continue;

        // Set height and add to queue
        heights[newRow][newCol] = heights[currentRow][currentCol] + 1;
        cellsToProcess.emplace(newRow, newCol);
      }
    }

    return heights;
  }
};

from collections import deque

class Solution:
    def highestPeak(self, isWater: list[list[int]]) -> list[list[int]]:
        directions = [(0, 1), (1, 0), (0, -1), (-1, 0)]
        rows = len(isWater)
        cols = len(isWater[0])
        heights = [[-1] * cols for _ in range(rows)]
        cellsToProcess = deque()

        # Initialize queue with all water cells and set their height to 0
        for row in range(rows):
            for col in range(cols):
                if isWater[row][col] == 1:
                    cellsToProcess.append((row, col))
                    heights[row][col] = 0

        # Perform BFS to calculate the height of each land cell
        while cellsToProcess:
            currentRow, currentCol = cellsToProcess.popleft()

            for dx, dy in directions:
                newRow = currentRow + dx
                newCol = currentCol + dy

                # Skip invalid or already-processed cells
                if newRow < 0 or newRow >= rows or newCol < 0 or newCol >= cols:
                    continue
                if heights[newRow][newCol] != -1:
                    continue

                # Set height and add to queue
                heights[newRow][newCol] = heights[currentRow][currentCol] + 1
                cellsToProcess.append((newRow, newCol))

        return heights

Time Complexity:

• Initialization:

  Iterating through the grid to initialize the queue with water cells takes \( O(m \times n) \), where \( m \) is the number of rows and \( n \) is the number of columns.

• BFS Traversal:

  Each cell is visited exactly once, and its neighbors are processed in \( O(1) \) time. The total cost of BFS traversal is \( O(m \times n) \).

• Overall Time Complexity:

  The overall time complexity is \( O(m \times n) \).

Space Complexity:

• Queue:

  The BFS queue stores at most \( O(m \times n) \) cells in the worst case, resulting in a space complexity of \( O(m \times n) \).

• Auxiliary Structures:

  The heights matrix also requires \( O(m \times n) \) space.

• Overall Space Complexity:

  The total space complexity is \( O(m \times n) \) due to the queue and the heights matrix.