1791. Find Center of Star Graph

There is an undirected star graph consisting of n nodes labeled from 1 to n. A star graph is a graph where there is one center node and exactly n - 1 edges that connect the center node with every other node.

You are given a 2D integer array edges where each edges[i] = [ui, vi] indicates that there is an edge between the nodes ui and vi. Return the center of the given star graph.

Example 1:

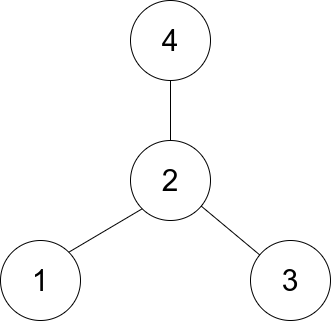
Input: edges = [[1,2],[2,3],[4,2]]
Output: 2
Explanation: As shown in the figure above, node 2 is connected to every other node, so 2 is the center.

Example 2:

Input: edges = [[1,2],[5,1],[1,3],[1,4]]
Output: 1

Constraints:

• 3 <= n <= 105
• edges.length == n - 1
• edges[i].length == 2
• 1 <= ui, vi <= n
• ui != vi
• The given edges represent a valid star graph.

Approach 01:

class Solution {
public:
    int findCenter(vector<vector<int>>& edges) {
        return edges[0][0] == edges[1][0] || edges[0][0] == edges[1][1] ? edges[0][0]: edges[0][1];
    }
};

class Solution:
    def findCenter(self, edges: List[List[int]]) -> int:
        if edges[0][0] in edges[1]:
            return edges[0][0]
        return edges[0][1]

Time Complexity

• The function checks a few conditions to determine the center node of the star graph.
• It performs constant-time operations, such as comparisons and assignments.
• Therefore, the time complexity is O(1).

Space Complexity

• The function does not use any additional space that scales with the size of the input.
• It only uses a few variables to store the intermediate results.
• Therefore, the space complexity is O(1).