Given the head of a linked list, remove the nth node from the end of the list and return its head.
Example 1:
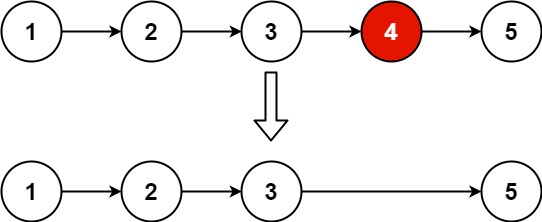
Input: head = [1,2,3,4,5], n = 2 Output: [1,2,3,5]
Example 2:
Input: head = [1], n = 1 Output: []
Example 3:
Input: head = [1,2], n = 1 Output: [1]
Constraints:
- The number of nodes in the list is
sz. 1 <= sz <= 300 <= Node.val <= 1001 <= n <= sz
Approach 01:
-
C++
-
Python
#include <bits/stdc++.h>
using namespace std;
struct ListNode {
int val;
ListNode *next;
ListNode() : val(0), next(nullptr) {}
ListNode(int x) : val(x), next(nullptr) {}
ListNode(int x, ListNode *next) : val(x), next(next) {}
};
class Solution {
public:
ListNode* removeNthFromEnd(ListNode* head, int n) {
int cnt = 0;
ListNode* temp = head;
while(temp != NULL){
cnt++;
temp = temp->next;
}
if(cnt == n){
ListNode* prev = NULL;
prev = head->next;
delete(head);
head = prev;
return head;
}
temp = head;
ListNode* prev = NULL;
int target = cnt-n+1;
cnt = 0;
while(temp!=NULL){
cnt++;
if(cnt == target){
prev->next = temp->next;
delete(temp);
break;
}
prev = temp;
temp = temp->next;
}
return head;
}
};
from typing import *
class ListNode:
def __init__(self, val=0, next=None):
self.val = val
self.next = next
class Solution:
def removeNthFromEnd(self, head: Optional[ListNode], n: int) -> Optional[ListNode]:
cnt = 0
temp = head
while(temp != None):
cnt += 1
temp = temp.next
if(cnt == n):
prev = head.next
del head
head = prev
return head
temp = head
prev = None
target = cnt - n + 1
cnt = 0
while(temp != None):
cnt += 1
if(cnt == target):
prev.next = temp.next
del temp
break
prev = temp
temp = temp.next
return head
Time Complexity:
The time complexity of the removeNthFromEnd method is \( O(L) \), where \( L \) is the number of nodes in the linked list.
- Traversal: Two passes through the linked list:
- First Pass: To count the total number of nodes \( L \). This is \( O(L) \).
- Second Pass: To reach the node just before the node to be deleted (which is \( L – n \)th node from the start). This is \( O(L) \).
Therefore, the total time complexity is \( O(L + L) = O(L) \).
Space Complexity:
The space complexity of the removeNthFromEnd method is \( O(1) \).
- Auxiliary Space: The method uses a constant amount of extra space regardless of the size of the input linked list. Variables like
cnt,temp,prev, andtargetare all constants in terms of space usage.
Hence, the space complexity remains \( O(1) \).