1905. Count Sub Islands

You are given two m x n binary matrices grid1 and grid2 containing only 0‘s (representing water) and 1‘s (representing land). An island is a group of 1‘s connected 4-directionally (horizontal or vertical). Any cells outside of the grid are considered water cells.

An island in grid2 is considered a sub-island if there is an island in grid1 that contains all the cells that make up this island in grid2.

Return the number of islands in grid2 that are considered sub-islands.

Example 1:

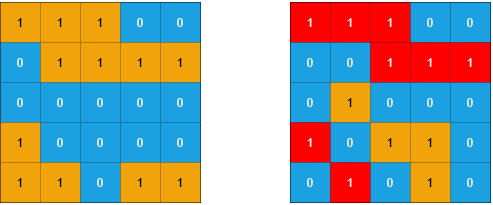
Input: grid1 = [[1,1,1,0,0],[0,1,1,1,1],[0,0,0,0,0],[1,0,0,0,0],[1,1,0,1,1]], grid2 = [[1,1,1,0,0],[0,0,1,1,1],[0,1,0,0,0],[1,0,1,1,0],[0,1,0,1,0]]
Output: 3
Explanation: In the picture above, the grid on the left is grid1 and the grid on the right is grid2.
The 1s colored red in grid2 are those considered to be part of a sub-island. There are three sub-islands.

Example 2:

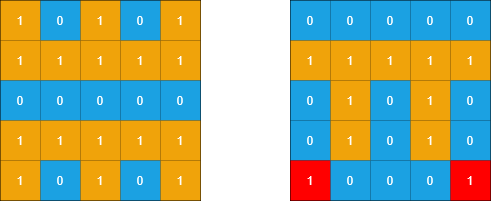
Input: grid1 = [[1,0,1,0,1],[1,1,1,1,1],[0,0,0,0,0],[1,1,1,1,1],[1,0,1,0,1]], grid2 = [[0,0,0,0,0],[1,1,1,1,1],[0,1,0,1,0],[0,1,0,1,0],[1,0,0,0,1]]
Output: 2 
Explanation: In the picture above, the grid on the left is grid1 and the grid on the right is grid2.
The 1s colored red in grid2 are those considered to be part of a sub-island. There are two sub-islands.

Constraints:

• m == grid1.length == grid2.length
• n == grid1[i].length == grid2[i].length
• 1 <= m, n <= 500
• grid1[i][j] and grid2[i][j] are either 0 or 1.

Approach 01:

#include <bits/stdc++.h>

using namespace std;

class Solution {
public:
    int countSubIslands(vector<vector<int>>& grid1, vector<vector<int>>& grid2) {
        int subIslandsCount = 0;

        for (int row = 0; row < grid2.size(); ++row) {
            for (int col = 0; col < grid2[0].size(); ++col) {
                if (grid2[row][col] == 1) {
                    subIslandsCount += exploreIsland(grid1, grid2, row, col);
                }
            }
        }
        return subIslandsCount;
    }

private:
    int exploreIsland(const vector<vector<int>>& grid1, vector<vector<int>>& grid2, int row, int col) {
        if (row < 0 || row == grid1.size() || col < 0 || col == grid2[0].size()) {
            return 1;
        }
        if (grid2[row][col] != 1) {
            return 1;
        }

        grid2[row][col] = 2; // Mark as visited
        return exploreIsland(grid1, grid2, row + 1, col) & 
               exploreIsland(grid1, grid2, row - 1, col) & 
               exploreIsland(grid1, grid2, row, col + 1) & 
               exploreIsland(grid1, grid2, row, col - 1) & 
               grid1[row][col];
    }
};

from typing import List

class Solution:
    def countSubIslands(self, grid1: List[List[int]], grid2: List[List[int]]) -> int:
        subIslandsCount = 0

        for row in range(len(grid2)):
            for col in range(len(grid2[0])):
                if grid2[row][col] == 1:
                    subIslandsCount += self.exploreIsland(grid1, grid2, row, col)
        
        return subIslandsCount

    def exploreIsland(self, grid1: List[List[int]], grid2: List[List[int]], row: int, col: int) -> int:
        if row < 0 or row == len(grid1) or col < 0 or col == len(grid2[0]):
            return 1
        if grid2[row][col] != 1:
            return 1

        grid2[row][col] = 2  # Mark as visited
        return (
            self.exploreIsland(grid1, grid2, row + 1, col) &
            self.exploreIsland(grid1, grid2, row - 1, col) &
            self.exploreIsland(grid1, grid2, row, col + 1) &
            self.exploreIsland(grid1, grid2, row, col - 1) &
            grid1[row][col]
        )

Time Complexity

• Grid Traversal:

  Traversing each cell in grid2 takes \( O(\text{numRows} \times \text{numCols}) \) time, where numRows is the number of rows and numCols is the number of columns in the grid.

• Exploring Islands (DFS):

  Each cell that is part of an island triggers a depth-first search (DFS). In the worst case, DFS explores all connected land cells, leading to an overall complexity of \( O(\text{numRows} \times \text{numCols}) \) for all DFS calls combined.

• Overall Time Complexity:

  The overall time complexity is \( O(\text{numRows} \times \text{numCols}) \), dominated by the traversal and exploration of grid cells.

Space Complexity

• Recursion Stack:

  The space complexity of the recursion stack during DFS is \( O(\text{numRows} \times \text{numCols}) \) in the worst case, where the entire grid could be an island.

• Grid Storage:

  The input grids grid1 and grid2 require \( O(\text{numRows} \times \text{numCols}) \) space for storage, but this space is given as part of the input and not additional space.

• Overall Space Complexity:

  The overall space complexity is \( O(\text{numRows} \times \text{numCols}) \), primarily due to the recursion stack during DFS traversal.