1937. Maximum Number of Points with Cost

You are given an m x n integer matrix points (0-indexed). Starting with 0 points, you want to maximize the number of points you can get from the matrix.

To gain points, you must pick one cell in each row. Picking the cell at coordinates (r, c) will add points[r][c] to your score.

However, you will lose points if you pick a cell too far from the cell that you picked in the previous row. For every two adjacent rows r and r + 1 (where 0 <= r < m - 1), picking cells at coordinates (r, c1) and (r + 1, c2) will subtract abs(c1 - c2) from your score.

Return the maximum number of points you can achieve.

abs(x) is defined as:

• x for x >= 0.
• -x for x < 0.

Example 1:

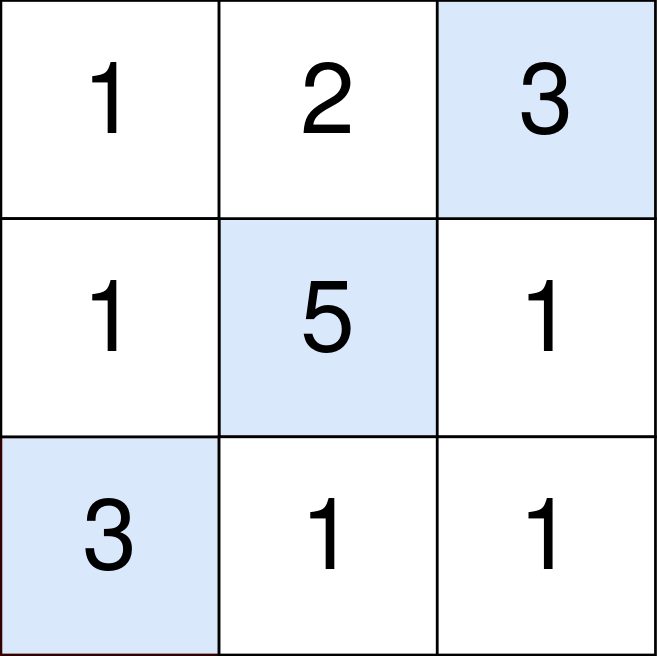
Input: points = [[1,2,3],[1,5,1],[3,1,1]]
Output: 9
Explanation:
The blue cells denote the optimal cells to pick, which have coordinates (0, 2), (1, 1), and (2, 0).
You add 3 + 5 + 3 = 11 to your score.
However, you must subtract abs(2 - 1) + abs(1 - 0) = 2 from your score.
Your final score is 11 - 2 = 9.

Example 2:

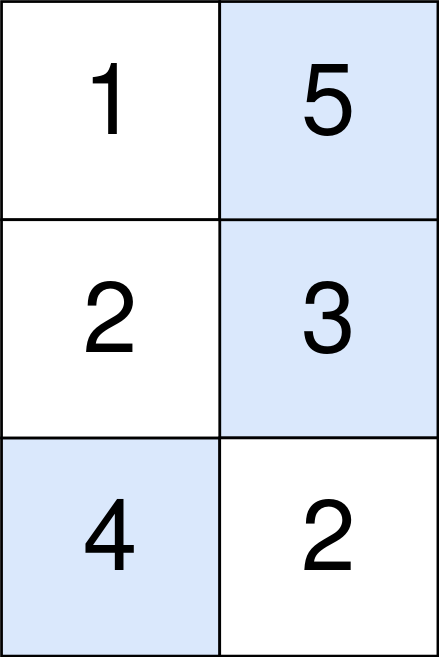
Input: points = [[1,5],[2,3],[4,2]]
Output: 11
Explanation:
The blue cells denote the optimal cells to pick, which have coordinates (0, 1), (1, 1), and (2, 0).
You add 5 + 3 + 4 = 12 to your score.
However, you must subtract abs(1 - 1) + abs(1 - 0) = 1 from your score.
Your final score is 12 - 1 = 11.

Constraints:

• m == points.length
• n == points[r].length
• 1 <= m, n <= 105
• 1 <= m * n <= 105
• 0 <= points[r][c] <= 105

Approach 01:

#include <vector>
#include <algorithm>
#include <ranges>

class Solution {
 public:
  long long maxPoints(std::vector<std::vector<int>>& points) {
    const int numCols = points[0].size();
    // dp[currentCol] := the maximum number of points you can have if points[i][currentCol] is the
    // most recent cell you picked
    std::vector<long> maxPointsForColumn(numCols);

    for (const std::vector<int>& row : points) {
      std::vector<long> maxPointsFromLeft(numCols);
      long currentMax = 0;

      // Calculate maximum points moving left to right
      for (int col = 0; col < numCols; ++col) {
        currentMax = std::max(currentMax - 1, maxPointsForColumn[col]);
        maxPointsFromLeft[col] = currentMax;
      }

      std::vector<long> maxPointsFromRight(numCols);
      currentMax = 0;

      // Calculate maximum points moving right to left
      for (int col = numCols - 1; col >= 0; --col) {
        currentMax = std::max(currentMax - 1, maxPointsForColumn[col]);
        maxPointsFromRight[col] = currentMax;
      }

      // Update the maximum points for each column considering both directions
      for (int col = 0; col < numCols; ++col)
        maxPointsForColumn[col] = std::max(maxPointsFromLeft[col], maxPointsFromRight[col]) + row[col];
    }

    return *std::ranges::max_element(maxPointsForColumn);
  }
};

from typing import List

class Solution:
    def maxPoints(self, points: List[List[int]]) -> int:
        numCols = len(points[0])
        # maxPointsForColumn[col] := the maximum number of points you can have if points[i][col] is the
        # most recent cell you picked
        maxPointsForColumn = [0] * numCols

        for row in points:
            maxPointsFromLeft = [0] * numCols
            currentMax = 0

            # Calculate maximum points moving left to right
            for col in range(numCols):
                currentMax = max(currentMax - 1, maxPointsForColumn[col])
                maxPointsFromLeft[col] = currentMax

            maxPointsFromRight = [0] * numCols
            currentMax = 0

            # Calculate maximum points moving right to left
            for col in range(numCols - 1, -1, -1):
                currentMax = max(currentMax - 1, maxPointsForColumn[col])
                maxPointsFromRight[col] = currentMax

            # Update the maximum points for each column considering both directions
            for col in range(numCols):
                maxPointsForColumn[col] = max(maxPointsFromLeft[col], maxPointsFromRight[col]) + row[col]

        return max(maxPointsForColumn)

Time Complexity

• Outer Loop:

  The outer loop iterates over each row of the `points` matrix. If there are \( m \) rows, this takes \( O(m) \) time.

• First Inner Loop (Left to Right):

  This loop iterates over each column in the current row to calculate `maxPointsFromLeft`. If there are \( n \) columns, this takes \( O(n) \) time.

• Second Inner Loop (Right to Left):

  This loop also iterates over each column to calculate `maxPointsFromRight`, taking \( O(n) \) time.

• Update Loop:

  The loop that updates `maxPointsForColumn` iterates over all columns, taking \( O(n) \) time.

• Overall Time Complexity:

  The function performs \( O(m) \) outer iterations and \( O(n) \) inner iterations, leading to an overall time complexity of \( O(m \times n) \).

Space Complexity

• Space for `maxPointsForColumn`:

  The function uses a vector of size \( n \) to store the maximum points for each column, which requires \( O(n) \) space.

• Space for `maxPointsFromLeft` and `maxPointsFromRight`:

  Two additional vectors of size \( n \) are used to store temporary values while processing each row, each requiring \( O(n) \) space.

• Overall Space Complexity:

  The overall space complexity is \( O(n) \) because the space used scales linearly with the number of columns.