2054. Two Best Non-Overlapping Events

You are given a 0-indexed 2D integer array of events where events[i] = [startTimei, endTimei, valuei]. The ith event starts at startTimeiand ends at endTimei, and if you attend this event, you will receive a value of valuei. You can choose at most two non-overlapping events to attend such that the sum of their values is maximized.

Return this maximum sum.

Note that the start time and end time is inclusive: that is, you cannot attend two events where one of them starts and the other ends at the same time. More specifically, if you attend an event with end time t, the next event must start at or after t + 1.

Example 1:

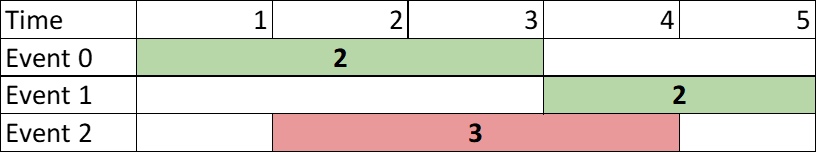
Input: events = [[1,3,2],[4,5,2],[2,4,3]]
Output: 4
Explanation: Choose the green events, 0 and 1 for a sum of 2 + 2 = 4.

Example 2:

Input: events = [[1,3,2],[4,5,2],[1,5,5]]
Output: 5
Explanation: Choose event 2 for a sum of 5.

Example 3:

Input: events = [[1,5,3],[1,5,1],[6,6,5]]
Output: 8
Explanation: Choose events 0 and 2 for a sum of 3 + 5 = 8.

Constraints:

• 2 <= events.length <= 105
• events[i].length == 3
• 1 <= startTimei <= endTimei <= 109
• 1 <= valuei <= 106

Approach 01:

class Solution {
public:
    int maxTwoEvents(vector<vector<int>>& events) {
        vector<tuple<int, int, int>> timeline;
        for (const auto& event : events) {
            int start = event[0];
            int end = event[1];
            int value = event[2];
            timeline.emplace_back(start, 1, value);  // Start of an event
            timeline.emplace_back(end + 1, -1, value);  // End of an event
        }
        sort(timeline.begin(), timeline.end());  // Sort by time
        
        int maxEventValue = 0;  // Maximum value of a single event seen so far
        int maxCombinedValue = 0;  // Best value of combining two events
        
        for (const auto& [time, eventType, eventValue] : timeline) {
            if (eventType == 1) {  // Start of an event
                maxCombinedValue = max(maxCombinedValue, maxEventValue + eventValue);
            } else if (eventType == -1) {  // End of an event
                maxEventValue = max(maxEventValue, eventValue);
            }
        }
        
        return maxCombinedValue;
    }
};

class Solution:
    def maxTwoEvents(self, events: List[List[int]]) -> int:
        timeline = []
        for start, end, value in events:
            timeline.append((start, 1, value))  # Add the start of an event
            timeline.append((end + 1, -1, value))  # Add the end of an event
        timeline.sort()  # Sort by time
        
        maxEventValue = 0  # Maximum value of a single event seen so far
        maxCombinedValue = 0  # Best value of combining two events
        
        for time, eventType, eventValue in timeline:
            if eventType == 1:  # Start of an event
                maxCombinedValue = max(maxCombinedValue, maxEventValue + eventValue)
            elif eventType == -1:  # End of an event
                maxEventValue = max(maxEventValue, eventValue)
        
        return maxCombinedValue

Time Complexity

• Building the Timeline:
  • For each event, two entries are added to the timeline (start and end+1).
  • Processing \(n\) events takes \(O(n)\).
• Sorting:
  • The timeline is sorted based on time, which involves \(2n\) entries.
  • Sorting takes \(O(2n \log(2n))\), simplified to \(O(n \log n)\).
• Traversal:
  • The sorted timeline is traversed once to compute the result.
  • This traversal takes \(O(2n)\), simplified to \(O(n)\).
• Overall Time Complexity:

  The total time complexity is \(O(n \log n)\), dominated by the sorting step.

Space Complexity

• Timeline Storage:
  • The timeline stores \(2n\) entries for \(n\) events.
  • This requires \(O(2n)\), simplified to \(O(n)\) space.
• Sorting Auxiliary Space:
  • Sorting the timeline requires \(O(n)\) additional space for the sorting algorithm (depending on the implementation).
• Other Variables:
  • Variables like maxEventValue, maxCombinedValue, and the loop variables require \(O(1)\) space.
• Overall Space Complexity:

  The space complexity is \(O(n)\), dominated by the timeline storage.