A critical point in a linked list is defined as either a local maxima or a local minima.
A node is a local maxima if the current node has a value strictly greater than the previous node and the next node.
A node is a local minima if the current node has a value strictly smaller than the previous node and the next node.
Note that a node can only be a local maxima/minima if there exists both a previous node and a next node.
Given a linked list head, return an array of length 2 containing [minDistance, maxDistance] where minDistance is the minimum distance between any two distinct critical points and maxDistance is the maximum distance between any two distinct critical points. If there are fewer than two critical points, return [-1, -1].
Example 1:
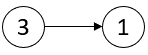
Input: head = [3,1] Output: [-1,-1] Explanation: There are no critical points in [3,1].
Example 2:

Input: head = [5,3,1,2,5,1,2] Output: [1,3] Explanation: There are three critical points: - [5,3,1,2,5,1,2]: The third node is a local minima because 1 is less than 3 and 2. - [5,3,1,2,5,1,2]: The fifth node is a local maxima because 5 is greater than 2 and 1. - [5,3,1,2,5,1,2]: The sixth node is a local minima because 1 is less than 5 and 2. The minimum distance is between the fifth and the sixth node. minDistance = 6 - 5 = 1. The maximum distance is between the third and the sixth node. maxDistance = 6 - 3 = 3.
Example 3:
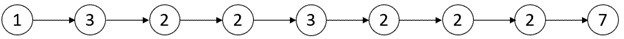
Input: head = [1,3,2,2,3,2,2,2,7] Output: [3,3] Explanation: There are two critical points: - [1,3,2,2,3,2,2,2,7]: The second node is a local maxima because 3 is greater than 1 and 2. - [1,3,2,2,3,2,2,2,7]: The fifth node is a local maxima because 3 is greater than 2 and 2. Both the minimum and maximum distances are between the second and the fifth node. Thus, minDistance and maxDistance is 5 - 2 = 3. Note that the last node is not considered a local maxima because it does not have a next node.
Constraints:
- The number of nodes in the list is in the range
[2, 105]. 1 <= Node.val <= 105
Approach 01:
-
C++
-
Python
#include <vector>
#include <limits>
using namespace std;
class Solution {
public:
vector<int> nodesBetweenCriticalPoints(ListNode* head) {
int min_distance = numeric_limits<int>::max();
int first_critical_index = -1;
int prev_critical_index = -1;
int index = 1;
ListNode* prev_node = head; // Pointer to the current node.
ListNode* curr_node = head->next; // Pointer to the next node.
while (curr_node->next) {
// Check for critical points (local maxima or minima).
if ((curr_node->val > prev_node->val && curr_node->val > curr_node->next->val) ||
(curr_node->val < prev_node->val && curr_node->val < curr_node->next->val)) {
// First critical index (only set once).
if (first_critical_index == -1) {
first_critical_index = index;
}
// Calculate minimum distance between consecutive critical points.
if (prev_critical_index != -1) {
min_distance = min(min_distance, index - prev_critical_index);
}
prev_critical_index = index;
}
prev_node = curr_node;
curr_node = curr_node->next;
++index;
}
if (min_distance == numeric_limits<int>::max()) {
return {-1, -1}; // No critical points found.
}
// Calculate distance between the first and last critical points.
int max_distance = prev_critical_index - first_critical_index;
return {min_distance, max_distance};
}
};
// Helper function to create a linked list
ListNode* create_list(vector<int>& values) {
ListNode* dummy = new ListNode(0);
ListNode* current = dummy;
for (int val : values) {
current->next = new ListNode(val);
current = current->next;
}
return dummy->next;
}
class Solution:
def nodesBetweenCriticalPoints(self, head: Optional[ListNode]) -> List[int]:
import sys
min_distance = sys.maxsize
first_critical_index = -1
prev_critical_index = -1
index = 1
prev_node = head # Pointer to the current node.
curr_node = head.next # Pointer to the next node.
while curr_node and curr_node.next:
# Check for critical points (local maxima or minima).
if (curr_node.val > prev_node.val and curr_node.val > curr_node.next.val) or \
(curr_node.val < prev_node.val and curr_node.val < curr_node.next.val):
# First critical index (only set once).
if first_critical_index == -1:
first_critical_index = index
# Calculate minimum distance between consecutive critical points.
if prev_critical_index != -1:
min_distance = min(min_distance, index - prev_critical_index)
prev_critical_index = index
prev_node = curr_node
curr_node = curr_node.next
index += 1
if min_distance == sys.maxsize:
return [-1, -1] # No critical points found.
# Calculate distance between the first and last critical points.
max_distance = prev_critical_index - first_critical_index
return [min_distance, max_distance]
# Helper function to create a linked list
def create_list(values: List[int]) -> ListNode:
dummy = ListNode(0)
current = dummy
for val in values:
current.next = ListNode(val)
current = current.next
return dummy.next
Time Complexity
-
Traversal:
Iterates through each node of the linked list once, so \( O(n) \), where \( n \) is the number of nodes.
-
Checking Critical Points:
For each node (except the last one), checks conditions and updates variables in constant time, \( O(1) \) per node.
-
Sorting the Edges:
Since there’s no sorting involved, this step doesn’t contribute to time complexity.
-
Overall Time Complexity:
The dominant factor is the traversal of the linked list, \( O(n) \).
Space Complexity
-
Additional Space:
Uses a few extra integer variables and pointers, \( O(1) \) additional space.
-
UnionFind Objects:
Each UnionFind object uses \( O(n) \) space, and we have two such objects, so total space is \( O(n) \).
-
Edges Vector:
The `edges` vector uses \( O(E) \) space, but it’s not applicable here.
-
Overall Space Complexity:
The space complexity is dominated by the variables and pointers used, \( O(1) \).