2096. Step-By-Step Directions From a Binary Tree Node to Another

You are given the root of a binary tree with n nodes. Each node is uniquely assigned a value from 1 to n. You are also given an integer startValue representing the value of the start node s, and a different integer destValue representing the value of the destination node t.

Find the shortest path starting from node s and ending at node t. Generate step-by-step directions of such path as a string consisting of only the uppercase letters 'L', 'R', and 'U'. Each letter indicates a specific direction:

• 'L' means to go from a node to its left child node.
• 'R' means to go from a node to its right child node.
• 'U' means to go from a node to its parent node.

Return the step-by-step directions of the shortest path from node s to node t.

Example 1:

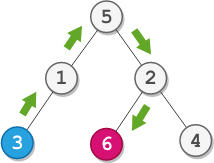
Input: root = [5,1,2,3,null,6,4], startValue = 3, destValue = 6
Output: "UURL"
Explanation: The shortest path is: 3 → 1 → 5 → 2 → 6.

Example 2:

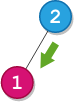
Input: root = [2,1], startValue = 2, destValue = 1
Output: "L"
Explanation: The shortest path is: 2 → 1.

Constraints:

• The number of nodes in the tree is n.
• 2 <= n <= 105
• 1 <= Node.val <= n
• All the values in the tree are unique.
• 1 <= startValue, destValue <= n
• startValue != destValue

Approach 01:

class Solution {
public:
    string getDirections(TreeNode* root, int startValue, int destValue) {
        string currentPath;
        string pathToStart;
        string pathToDest;

        // Find the lowest common ancestor and start DFS from there.
        dfs(findLCA(root, startValue, destValue), startValue, destValue, currentPath, pathToStart, pathToDest);

        // Construct the path by going up to the common ancestor and then down to the destination.
        return string(pathToStart.length(), 'U') + pathToDest;
    }

private:
    // Function to find the lowest common ancestor (LCA) of two nodes.
    TreeNode* findLCA(TreeNode* root, int p, int q) {
        if (root == nullptr || root->val == p || root->val == q) {
            return root;
        }

        TreeNode* leftLCA = findLCA(root->left, p, q);
        TreeNode* rightLCA = findLCA(root->right, p, q);

        if (leftLCA != nullptr && rightLCA != nullptr) {
            return root;
        }

        return leftLCA == nullptr ? rightLCA : leftLCA;
    }

    // DFS to find paths from the LCA to the start and destination nodes.
    void dfs(TreeNode* root, int startValue, int destValue, string& currentPath, string& pathToStart, string& pathToDest) {
        if (root == nullptr) {
            return;
        }

        if (root->val == startValue) {
            pathToStart = currentPath;
        }

        if (root->val == destValue) {
            pathToDest = currentPath;
        }

        // Traverse left subtree
        currentPath.push_back('L');
        dfs(root->left, startValue, destValue, currentPath, pathToStart, pathToDest);
        currentPath.pop_back();

        // Traverse right subtree
        currentPath.push_back('R');
        dfs(root->right, startValue, destValue, currentPath, pathToStart, pathToDest);
        currentPath.pop_back();
    }
};

class Solution:
    def getDirections(self, root: TreeNode, startValue: int, destValue: int) -> str:
        currentPath = []
        pathToStart = []
        pathToDest = []

        # Find the lowest common ancestor and start DFS from there.
        self.dfs(self.findLCA(root, startValue, destValue), startValue, destValue, currentPath, pathToStart, pathToDest)

        # Construct the path by going up to the common ancestor and then down to the destination.
        return 'U' * len(pathToStart) + ''.join(pathToDest)

    # Function to find the lowest common ancestor (LCA) of two nodes.
    def findLCA(self, root: TreeNode, p: int, q: int) -> TreeNode:
        if root is None or root.val == p or root.val == q:
            return root

        leftLCA = self.findLCA(root.left, p, q)
        rightLCA = self.findLCA(root.right, p, q)

        if leftLCA is not None and rightLCA is not None:
            return root

        return leftLCA if leftLCA is not None else rightLCA

    # DFS to find paths from the LCA to the start and destination nodes.
    def dfs(self, root: TreeNode, startValue: int, destValue: int, currentPath: list, pathToStart: list, pathToDest: list):
        if root is None:
            return

        if root.val == startValue:
            pathToStart.extend(currentPath)
        if root.val == destValue:
            pathToDest.extend(currentPath)

        # Traverse left subtree
        currentPath.append('L')
        self.dfs(root.left, startValue, destValue, currentPath, pathToStart, pathToDest)
        currentPath.pop()

        # Traverse right subtree
        currentPath.append('R')
        self.dfs(root.right, startValue, destValue, currentPath, pathToStart, pathToDest)
        currentPath.pop()

Time Complexity

• Finding the Lowest Common Ancestor (LCA):

  The findLCA function traverses the tree to find the lowest common ancestor of the start and destination nodes. In the worst case, this traversal visits all nodes, resulting in \( O(n) \) time complexity, where \( n \) is the number of nodes in the tree.

• Depth-First Search (DFS):

  The dfs function is called to find paths from the LCA to both the start and destination nodes. In the worst case, this traversal also visits all nodes, resulting in \( O(n) \) time complexity.

• Overall Time Complexity:

  The overall time complexity is \( O(n) + O(n) = O(n) \).

Space Complexity

• Auxiliary Space for Recursion:

  The recursive calls for both findLCA and dfs functions use the call stack. In the worst case, the depth of the recursion stack can be \( O(h) \), where \( h \) is the height of the tree. For a balanced binary tree, \( h = \log n \), and for a skewed binary tree, \( h = n \).

• Additional Data Structures:

  Using currentPath, pathToStart, and pathToDest requires additional space, but this space is proportional to the height of the tree. Therefore, it is \( O(h) \).

• Overall Space Complexity:

  The overall space complexity is \( O(h) \). For a balanced tree, it is \( O(\log n) \), and for a skewed tree, it is \( O(n) \).