2116. Check if a Parentheses String Can Be Valid

A parentheses string is a non-empty string consisting only of '(' and ')'. It is valid if any of the following conditions is true:

• It is ().
• It can be written as AB (A concatenated with B), where A and B are valid parentheses strings.
• It can be written as (A), where A is a valid parentheses string.

You are given a parentheses string s and a string locked, both of length n. locked is a binary string consisting only of '0's and '1's. For each index i of locked,

• If locked[i] is '1', you cannot change s[i].
• But if locked[i] is '0', you can change s[i] to either '(' or ')'.

Return true if you can make s a valid parentheses string. Otherwise, return false.

Example 1:

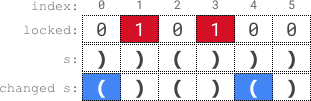
Input: s = "))()))", locked = "010100"
Output: true
Explanation: locked[1] == '1' and locked[3] == '1', so we cannot change s[1] or s[3].
We change s[0] and s[4] to '(' while leaving s[2] and s[5] unchanged to make s valid.

Example 2:

Input: s = "()()", locked = "0000"
Output: true
Explanation: We do not need to make any changes because s is already valid.

Example 3:

Input: s = ")", locked = "0"
Output: false
Explanation: locked permits us to change s[0].
Changing s[0] to either '(' or ')' will not make s valid.

Constraints:

• n == s.length == locked.length
• 1 <= n <= 105
• s[i] is either '(' or ')'.
• locked[i] is either '0' or '1'.

Approach 01:

#include <string>
#include <algorithm>
using namespace std;

class Solution {
public:
  bool canBeValid(string brackets, string locked) {
    // If the length of the string is odd, it's impossible to make valid parentheses
    if (brackets.length() % 2 == 1)
      return false;

    // Check both directions: left-to-right and right-to-left
    const bool leftToRightIsValid = validateBrackets(brackets, locked, true);
    reverse(brackets.begin(), brackets.end());
    reverse(locked.begin(), locked.end());
    const bool rightToLeftIsValid = validateBrackets(brackets, locked, false);

    return leftToRightIsValid && rightToLeftIsValid;
  }

private:
  bool validateBrackets(const string& brackets, const string& locked, bool isForward) {
    int changeableCount = 0; // Count of brackets that can be changed
    int openCount = 0;       // Count of open brackets
    int closeCount = 0;      // Count of close brackets

    for (int i = 0; i < brackets.length(); ++i) {
      const char currentBracket = brackets[i];
      const char isLocked = locked[i];

      if (isLocked == '0') {
        ++changeableCount; // Bracket can be changed
      } else if (currentBracket == '(') {
        ++openCount; // Count open brackets
      } else { // currentBracket == ')'
        ++closeCount; // Count close brackets
      }

      // Check if it's valid based on the current counts
      if (isForward && changeableCount + openCount - closeCount < 0)
        return false;
      if (!isForward && changeableCount + closeCount - openCount < 0)
        return false;
    }

    return true;
  }
};

class Solution:
    def canBeValid(self, brackets: str, locked: str) -> bool:
        # If the length of the string is odd, it's impossible to make valid parentheses
        if len(brackets) % 2 == 1:
            return False

        # Check both directions: left-to-right and right-to-left
        leftToRightIsValid = self._validateBrackets(brackets, locked, isForward=True)
        brackets = brackets[::-1]
        locked = locked[::-1]
        rightToLeftIsValid = self._validateBrackets(brackets, locked, isForward=False)

        return leftToRightIsValid and rightToLeftIsValid

    def _validateBrackets(self, brackets: str, locked: str, isForward: bool) -> bool:
        changeableCount = 0  # Count of brackets that can be changed
        openCount = 0        # Count of open brackets
        closeCount = 0       # Count of close brackets

        for currentBracket, isLocked in zip(brackets, locked):
            if isLocked == '0':
                changeableCount += 1  # Bracket can be changed
            elif currentBracket == '(':
                openCount += 1  # Count open brackets
            else:  # currentBracket == ')'
                closeCount += 1  # Count close brackets

            # Check if it's valid based on the current counts
            if isForward and changeableCount + openCount - closeCount < 0:
                return False
            if not isForward and changeableCount + closeCount - openCount < 0:
                return False

        return True

Time Complexity:

• Processing Each Character:

  The algorithm iterates through the input string twice: once for the left-to-right validation and once for the right-to-left validation. Each iteration processes every character exactly once, resulting in \( O(n) \), where \( n \) is the length of the input string.

• Reversals:

  The reverse operations on the string and locked arrays also take \( O(n) \), but this cost is linear and happens only once per validation.

• Overall Time Complexity:

  \( O(n) \).

Space Complexity:

• Extra Variables:

  The algorithm uses a constant amount of extra space for variables like changeableCount, openCount, and closeCount.

• Input Modifications:

  Although the input strings are reversed, this does not require additional space beyond the original strings.

• Overall Space Complexity:

  \( O(1) \).