2196. Create Binary Tree From Descriptions

You are given a 2D integer array descriptions where descriptions[i] = [parenti, childi, isLefti] indicates that parenti is the parent of childi in a binary tree of unique values. Furthermore,

• If isLefti == 1, then childi is the left child of parenti.
• If isLefti == 0, then childi is the right child of parenti.

Construct the binary tree described by descriptions and return its root.

The test cases will be generated such that the binary tree is valid.

Example 1:

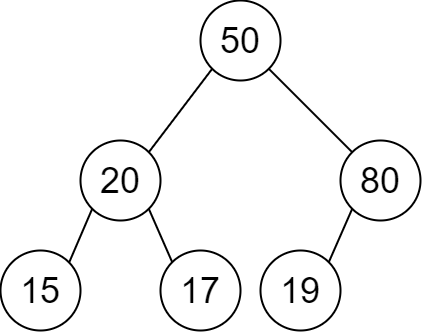
Input: descriptions = [[20,15,1],[20,17,0],[50,20,1],[50,80,0],[80,19,1]]
Output: [50,20,80,15,17,19]
Explanation: The root node is the node with value 50 since it has no parent.
The resulting binary tree is shown in the diagram.

Example 2:

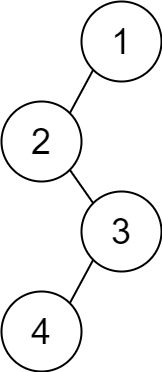
Input: descriptions = [[1,2,1],[2,3,0],[3,4,1]]
Output: [1,2,null,null,3,4]
Explanation: The root node is the node with value 1 since it has no parent.
The resulting binary tree is shown in the diagram.

Constraints:

• 1 <= descriptions.length <= 104
• descriptions[i].length == 3
• 1 <= parenti, childi <= 105
• 0 <= isLefti <= 1
• The binary tree described by descriptions is valid.

Approach 01:

class Solution {
public:
    TreeNode* createBinaryTree(vector<vector<int>>& descriptions) {
        unordered_map<TreeNode*, TreeNode*> childToParentMap;
        unordered_map<int, TreeNode*> valueToNodeMap;

        for (const vector<int>& description : descriptions) {
            const int parentValue = description[0];
            const int childValue = description[1];
            const bool isLeftChild = description[2];

            TreeNode* parentNode = valueToNodeMap.count(parentValue) ? valueToNodeMap[parentValue] : (valueToNodeMap[parentValue] = new TreeNode(parentValue));
            TreeNode* childNode = valueToNodeMap.count(childValue) ? valueToNodeMap[childValue] : (valueToNodeMap[childValue] = new TreeNode(childValue));

            childToParentMap[childNode] = parentNode;

            if (isLeftChild){
                parentNode->left = childNode;
            }
            else{
                parentNode->right = childNode;
            }
        }

        // Pick a random node and traverse upward to find the root.
        TreeNode* root = childToParentMap.begin()->second;
        while (childToParentMap.count(root)){
            root = childToParentMap[root];
        }
        return root;
    }
};

from typing import List
from collections import defaultdict

# Definition for a binary tree node.
class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

class Solution:
    def createBinaryTree(self, descriptions: List[List[int]]) -> TreeNode:
        childToParentMap = {}
        valueToNodeMap = {}

        for description in descriptions:
            parentValue = description[0]
            childValue = description[1]
            isLeftChild = description[2]

            if parentValue not in valueToNodeMap:
                valueToNodeMap[parentValue] = TreeNode(parentValue)
            parentNode = valueToNodeMap[parentValue]

            if childValue not in valueToNodeMap:
                valueToNodeMap[childValue] = TreeNode(childValue)
            childNode = valueToNodeMap[childValue]

            childToParentMap[childNode] = parentNode

            if isLeftChild:
                parentNode.left = childNode
            else:
                parentNode.right = childNode

        # Pick a random node and traverse upward to find the root.
        root = next(iter(childToParentMap.values()))
        while root in childToParentMap:
            root = childToParentMap[root]

        return root

Time Complexity

• Initialization and Input Handling:

  Iterating through the descriptions vector takes \( O(n) \) time, where \( n \) is the number of descriptions.

• Node Creation and Mapping:

  For each description, checking and creating nodes in the valueToNodeMap and updating the childToParentMap takes \( O(1) \) time. Since there are \( n \) descriptions, this part also takes \( O(n) \) time.

• Finding the Root:

  Traversing from a random node upwards to find the root takes \( O(h) \) time, where \( h \) is the height of the tree. In the worst case, \( h \) can be \( O(n) \), but typically it’s much smaller.

• Overall Time Complexity:

  The overall time complexity is \( O(n) \).

Space Complexity

• Auxiliary Space:

  Storing the childToParentMap and valueToNodeMap uses additional space. Both maps can contain up to \( O(n) \) entries, where \( n \) is the number of nodes, leading to \( O(n) \) space usage.

• Node Creation:

  Creating nodes also requires \( O(n) \) space, where \( n \) is the number of nodes in the tree.

• Overall Space Complexity:

  The overall space complexity is \( O(n) \).