You are given two integers m and n representing a 0-indexed m x n grid. You are also given two 2D integer arrays guards and walls where guards[i] = [rowi, coli] and walls[j] = [rowj, colj] represent the positions of the ith guard and jth wall respectively.
A guard can see every cell in the four cardinal directions (north, east, south, or west) starting from their position unless obstructed by a wall or another guard. A cell is guarded if there is at least one guard that can see it.
Return the number of unoccupied cells that are not guarded.
Example 1:
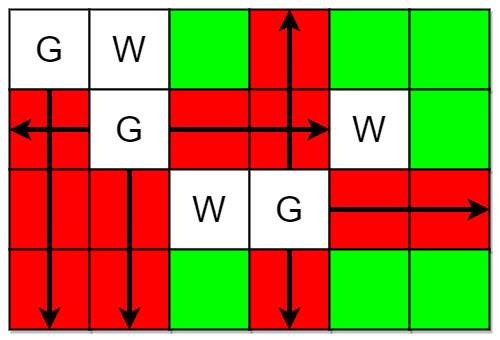
Input: m = 4, n = 6, guards = [[0,0],[1,1],[2,3]], walls = [[0,1],[2,2],[1,4]] Output: 7 Explanation: The guarded and unguarded cells are shown in red and green respectively in the above diagram. There are a total of 7 unguarded cells, so we return 7.
Example 2:
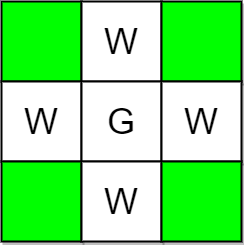
Input: m = 3, n = 3, guards = [[1,1]], walls = [[0,1],[1,0],[2,1],[1,2]] Output: 4 Explanation: The unguarded cells are shown in green in the above diagram. There are a total of 4 unguarded cells, so we return 4.
Constraints:
1 <= m, n <= 1052 <= m * n <= 1051 <= guards.length, walls.length <= 5 * 1042 <= guards.length + walls.length <= m * nguards[i].length == walls[j].length == 20 <= rowi, rowj < m0 <= coli, colj < n- All the positions in
guardsandwallsare unique.
Approach 01:
-
C++
-
Python
#include <vector>
using namespace std;
class Solution {
public:
int countUnguarded(int rows, int cols, vector<vector<int>>& guards, vector<vector<int>>& walls) {
int unguardedCount = 0;
vector<vector<char>> grid(rows, vector<char>(cols));
vector<vector<char>> leftGuard(rows, vector<char>(cols));
vector<vector<char>> rightGuard(rows, vector<char>(cols));
vector<vector<char>> upGuard(rows, vector<char>(cols));
vector<vector<char>> downGuard(rows, vector<char>(cols));
// Mark guards and walls on the grid
for (const vector<int>& guard : guards){
grid[guard[0]][guard[1]] = 'G';
}
for (const vector<int>& wall : walls){
grid[wall[0]][wall[1]] = 'W';
}
// Fill guard visibility from left and right
for (int i = 0; i < rows; ++i) {
char lastSeen = 0;
for (int j = 0; j < cols; ++j){
updateGuardInfo(grid[i][j], lastSeen, leftGuard[i][j]);
}
lastSeen = 0;
for (int j = cols - 1; j >= 0; --j){
updateGuardInfo(grid[i][j], lastSeen, rightGuard[i][j]);
}
}
// Fill guard visibility from top and bottom
for (int j = 0; j < cols; ++j) {
char lastSeen = 0;
for (int i = 0; i < rows; ++i){
updateGuardInfo(grid[i][j], lastSeen, upGuard[i][j]);
}
lastSeen = 0;
for (int i = rows - 1; i >= 0; --i){
updateGuardInfo(grid[i][j], lastSeen, downGuard[i][j]);
}
}
// Count unguarded cells
for (int i = 0; i < rows; ++i) {
for (int j = 0; j < cols; ++j) {
if (grid[i][j] == 0 && leftGuard[i][j] != 'G' &&
rightGuard[i][j] != 'G' && upGuard[i][j] != 'G' &&
downGuard[i][j] != 'G') {
++unguardedCount;
}
}
}
return unguardedCount;
}
private:
void updateGuardInfo(char currentCell, char& lastSeen, char& guardInfo) {
if (currentCell == 'G' || currentCell == 'W'){
lastSeen = currentCell;
}
else{
guardInfo = lastSeen;
}
}
};
from typing import List
class Solution:
def countUnguarded(self, rows: int, cols: int, guards: List[List[int]], walls: List[List[int]]) -> int:
unguardedCount = 0
grid = [[0] * cols for _ in range(rows)]
leftGuard = [[0] * cols for _ in range(rows)]
rightGuard = [[0] * cols for _ in range(rows)]
upGuard = [[0] * cols for _ in range(rows)]
downGuard = [[0] * cols for _ in range(rows)]
# Mark guards and walls on the grid
for guard in guards:
grid[guard[0]][guard[1]] = 'G'
for wall in walls:
grid[wall[0]][wall[1]] = 'W'
# Fill guard visibility from left and right
for i in range(rows):
lastSeen = 0
for j in range(cols):
lastSeen = self.updateGuardInfo(grid[i][j], lastSeen, leftGuard, i, j)
lastSeen = 0
for j in range(cols - 1, -1, -1):
lastSeen = self.updateGuardInfo(grid[i][j], lastSeen, rightGuard, i, j)
# Fill guard visibility from top and bottom
for j in range(cols):
lastSeen = 0
for i in range(rows):
lastSeen = self.updateGuardInfo(grid[i][j], lastSeen, upGuard, i, j)
lastSeen = 0
for i in range(rows - 1, -1, -1):
lastSeen = self.updateGuardInfo(grid[i][j], lastSeen, downGuard, i, j)
# Count unguarded cells
for i in range(rows):
for j in range(cols):
if (grid[i][j] == 0 and leftGuard[i][j] != 'G' and
rightGuard[i][j] != 'G' and upGuard[i][j] != 'G' and
downGuard[i][j] != 'G'):
unguardedCount += 1
return unguardedCount
def updateGuardInfo(self, currentCell: str, lastSeen: str, guardInfo: List[List[str]], i: int, j: int) -> str:
if currentCell in {'G', 'W'}:
lastSeen = currentCell
else:
guardInfo[i][j] = lastSeen
return lastSeen
Time Complexity
- Grid Initialization:
Initializing the grid with dimensions \( \text{rows} \times \text{cols} \) takes \( O(\text{rows} \times \text{cols}) \) time.
- Marking Guards and Walls:
Filling the grid with guards and walls requires iterating through the guard and wall lists. This takes \( O(g + w) \), where \( g \) is the number of guards and \( w \) is the number of walls.
- Filling Guard Visibility:
Filling guard visibility for each direction (left, right, up, down) requires four passes over the grid, each taking \( O(\text{rows} \times \text{cols}) \) time. This results in \( O(4 \times \text{rows} \times \text{cols}) = O(\text{rows} \times \text{cols}) \).
- Counting Unguarded Cells:
Finally, counting the unguarded cells requires a full grid scan, which takes \( O(\text{rows} \times \text{cols}) \).
- Overall Time Complexity:
The overall time complexity is \( O(\text{rows} \times \text{cols} + g + w) \). In practice, \( g + w \) is much smaller than \( \text{rows} \times \text{cols} \), so the complexity simplifies to \( O(\text{rows} \times \text{cols}) \).
Space Complexity
- Grid Storage:
The grid and auxiliary grids (leftGuard, rightGuard, upGuard, downGuard) all require \( O(\text{rows} \times \text{cols}) \) space.
- Auxiliary Variables:
Other variables like
unguardedCount,lastSeen, andguardInforequire \( O(1) \) space. - Overall Space Complexity:
The overall space complexity is \( O(\text{rows} \times \text{cols}) \), considering the storage required for the grid and auxiliary arrays.