2290. Minimum Obstacle Removal to Reach Corner

You are given a 0-indexed 2D integer array grid of size m x n. Each cell has one of two values:

• 0 represents an empty cell,
• 1 represents an obstacle that may be removed.

You can move up, down, left, or right from and to an empty cell.

Return the minimum number of obstacles to remove so you can move from the upper left corner (0, 0) to the lower right corner (m - 1, n - 1).

Example 1:

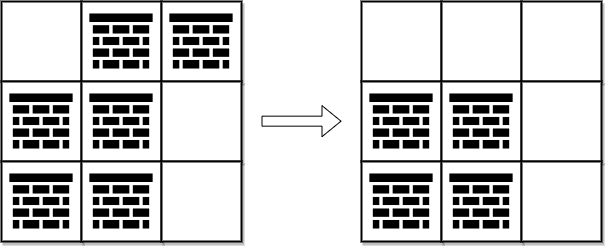
Input: grid = [[0,1,1],[1,1,0],[1,1,0]]
Output: 2
Explanation: We can remove the obstacles at (0, 1) and (0, 2) to create a path from (0, 0) to (2, 2).
It can be shown that we need to remove at least 2 obstacles, so we return 2.
Note that there may be other ways to remove 2 obstacles to create a path.

Example 2:

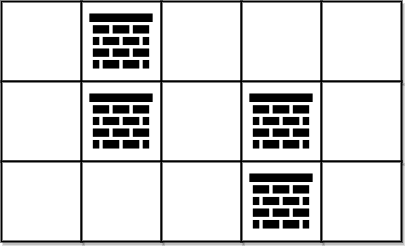
Input: grid = [[0,1,0,0,0],[0,1,0,1,0],[0,0,0,1,0]]
Output: 0
Explanation: We can move from (0, 0) to (2, 4) without removing any obstacles, so we return 0.

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 105
• 2 <= m * n <= 105
• grid[i][j] is either 0 or 1.
• grid[0][0] == grid[m - 1][n - 1] == 0

Approach 01:

class Solution {
 public:
  int minimumObstacles(vector<vector<int>>& grid) {
    const int rows = grid.size();
    const int cols = grid[0].size();
    constexpr int directions[4][2] = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
    using Cell = tuple<int, int, int>;  // (distance, row, col)
    priority_queue<Cell, vector<Cell>, greater<>> minHeap;
    vector<vector<int>> minDistance(rows, vector<int>(cols, INT_MAX));

    minHeap.emplace(grid[0][0], 0, 0);
    minDistance[0][0] = grid[0][0];

    while (!minHeap.empty()) {
      const auto [currentDistance, currentRow, currentCol] = minHeap.top();
      minHeap.pop();

      if (currentRow == rows - 1 && currentCol == cols - 1)
        return currentDistance;

      for (const auto& [dx, dy] : directions) {
        const int nextRow = currentRow + dx;
        const int nextCol = currentCol + dy;

        if (nextRow < 0 || nextRow >= rows || nextCol < 0 || nextCol >= cols)
          continue;

        const int newDistance = currentDistance + grid[nextRow][nextCol];
        if (newDistance < minDistance[nextRow][nextCol]) {
          minDistance[nextRow][nextCol] = newDistance;
          minHeap.emplace(newDistance, nextRow, nextCol);
        }
      }
    }

    return minDistance[rows - 1][cols - 1];
  }
};

from heapq import heappop, heappush
from typing import List, Tuple

class Solution:
    def minimumObstacles(self, grid: List[List[int]]) -> int:
        rows = len(grid)
        cols = len(grid[0])
        directions = [(0, 1), (1, 0), (0, -1), (-1, 0)]
        minHeap: List[Tuple[int, int, int]] = []  # (distance, row, col)
        minDistance = [[float('inf')] * cols for _ in range(rows)]

        heappush(minHeap, (grid[0][0], 0, 0))
        minDistance[0][0] = grid[0][0]

        while minHeap:
            currentDistance, currentRow, currentCol = heappop(minHeap)

            if currentRow == rows - 1 and currentCol == cols - 1:
                return currentDistance

            for dx, dy in directions:
                nextRow = currentRow + dx
                nextCol = currentCol + dy

                if nextRow < 0 or nextRow >= rows or nextCol < 0 or nextCol >= cols:
                    continue

                newDistance = currentDistance + grid[nextRow][nextCol]
                if newDistance < minDistance[nextRow][nextCol]:
                    minDistance[nextRow][nextCol] = newDistance
                    heappush(minHeap, (newDistance, nextRow, nextCol))

        return minDistance[rows - 1][cols - 1]

Time Complexity

• Heap operations:

  In the worst case, each cell in the grid could be visited and processed once. For each cell, the operations of inserting or updating in the heap take \(O(\log(k))\), where \(k\) is the number of elements in the heap. Since there are \(m \times n\) cells, where \(m\) is the number of rows and \(n\) is the number of columns, the time complexity of the heap operations is \(O((m \times n) \log(m \times n))\).

• Neighbor traversal:

  For each cell, up to 4 neighbors are checked, which takes constant time. This step is linear in the number of cells, contributing \(O(m \times n)\).

• Overall Time Complexity:

  The overall time complexity is \(O((m \times n) \log(m \times n))\), dominated by the heap operations.

Space Complexity

• Min-Heap:

  The heap can contain up to \(m \times n\) elements in the worst case, resulting in a space complexity of \(O(m \times n)\).

• Distance Matrix:

  The distance matrix minDistance has dimensions \(m \times n\), requiring \(O(m \times n)\) space.

• Overall Space Complexity:

  The overall space complexity is \(O(m \times n)\), where \(m\) is the number of rows and \(n\) is the number of columns.