2326. Spiral Matrix IV

You are given two integers m and n, which represent the dimensions of a matrix.

You are also given the head of a linked list of integers.

Generate an m x n matrix that contains the integers in the linked list presented in spiral order (clockwise), starting from the top-left of the matrix. If there are remaining empty spaces, fill them with -1.

Return the generated matrix.

Example 1:

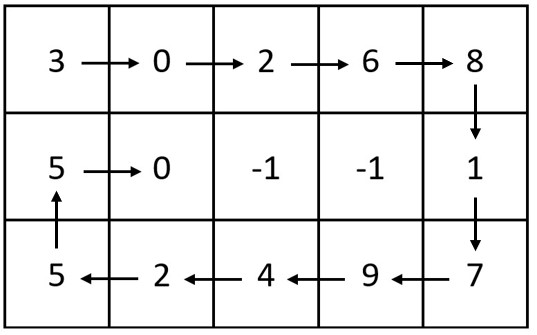
Input: m = 3, n = 5, head = [3,0,2,6,8,1,7,9,4,2,5,5,0]
Output: [[3,0,2,6,8],[5,0,-1,-1,1],[5,2,4,9,7]]
Explanation: The diagram above shows how the values are printed in the matrix.
Note that the remaining spaces in the matrix are filled with -1.

Example 2:

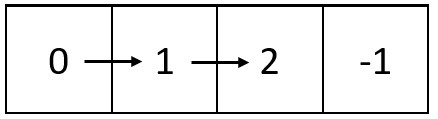
Input: m = 1, n = 4, head = [0,1,2]
Output: [[0,1,2,-1]]
Explanation: The diagram above shows how the values are printed from left to right in the matrix.
The last space in the matrix is set to -1.

Constraints:

• 1 <= m, n <= 105
• 1 <= m * n <= 105
• The number of nodes in the list is in the range [1, m * n].
• 0 <= Node.val <= 1000

Approach 01:

class Solution {
public:
    vector<vector<int>> spiralMatrix(int rows, int cols, ListNode* head) {
        // Directions for moving right, down, left, up
        constexpr int directionOffsets[4][2] = { {0, 1}, {1, 0}, {0, -1}, {-1, 0}};
        vector<vector<int>> matrix(rows, vector<int>(cols, -1));

        int currentRow = 0;     // Current row position
        int currentCol = 0;     // Current column position
        int directionIndex = 0; // Current direction index

        for (ListNode* node = head; node; node = node->next) {
            matrix[currentRow][currentCol] = node->val;

            // Check if we need to change direction
            if (currentRow + directionOffsets[directionIndex][0] < 0 ||
                currentRow + directionOffsets[directionIndex][0] == rows ||
                currentCol + directionOffsets[directionIndex][1] < 0 ||
                currentCol + directionOffsets[directionIndex][1] == cols ||
                matrix[currentRow + directionOffsets[directionIndex][0]] [currentCol + directionOffsets[directionIndex][1]] != -1) {
                directionIndex = (directionIndex + 1) % 4;
            }

            currentRow += directionOffsets[directionIndex][0];
            currentCol += directionOffsets[directionIndex][1];
        }

        return matrix;
    }
};

class ListNode:
    def __init__(self, val=0, next=None):
        self.val = val
        self.next = next

class Solution:
    def spiralMatrix(self, numRows: int, numCols: int, head: ListNode) -> list[list[int]]:
        # Directions for moving right, down, left, up
        directionOffsets = [(0, 1), (1, 0), (0, -1), (-1, 0)]
        matrix = [[-1] * numCols for _ in range(numRows)]

        currentRow = 0     # Current row position
        currentCol = 0     # Current column position
        directionIndex = 0 # Current direction index

        node = head
        while node:
            matrix[currentRow][currentCol] = node.val
            
            # Check if we need to change direction
            if (currentRow + directionOffsets[directionIndex][0] < 0 or
                currentRow + directionOffsets[directionIndex][0] == numRows or
                currentCol + directionOffsets[directionIndex][1] < 0 or
                currentCol + directionOffsets[directionIndex][1] == numCols or
                matrix[currentRow + directionOffsets[directionIndex][0]][currentCol + directionOffsets[directionIndex][1]] != -1):
                directionIndex = (directionIndex + 1) % 4

            currentRow += directionOffsets[directionIndex][0]
            currentCol += directionOffsets[directionIndex][1]
            node = node.next

        return matrix

Time Complexity

• Traversing the Linked List:

  The loop iterates through each node in the linked list once. If there are n nodes in the linked list, this operation takes \( O(n) \) time.

• Filling the Matrix:

  The matrix is filled in a spiral order, and each cell is visited once. If the matrix has r rows and c columns, the matrix filling operation takes \( O(r \times c) \) time. The matrix size is determined by the product of rows and columns, so this operation is also \( O(n) \), where n = \(r \times c\) .

• Overall Time Complexity:

  The overall time complexity is \( O(n) \), where n is the total number of cells in the matrix (i.e., \(r \times c\)), assuming the number of linked list nodes is equal to the number of matrix cells.

Space Complexity

• Matrix Storage:

  The matrix is stored in a 2D vector with \(r \times c\) cells, so the space complexity for the matrix is \( O(r \times c) \).

• Other Variables:

  The additional space used by variables (e.g., direction offsets, current row, and column indices) is \( O(1) \), which is constant and does not depend on the size of the input.

• Overall Space Complexity:

  The overall space complexity is \( O(r \times c) \), primarily due to the storage required for the matrix.