2458. Height of Binary Tree After Subtree Removal Queries

You are given the root of a binary tree with n nodes. Each node is assigned a unique value from 1 to n. You are also given an array queries of size m.

You have to perform m independent queries on the tree where in the ith query you do the following:

• Remove the subtree rooted at the node with the value queries[i] from the tree. It is guaranteed that queries[i] will not be equal to the value of the root.

Return an array answer of size m where answer[i] is the height of the tree after performing the ith query.

Note:

• The queries are independent, so the tree returns to its initial state after each query.
• The height of a tree is the number of edges in the longest simple path from the root to some node in the tree.

Example 1:

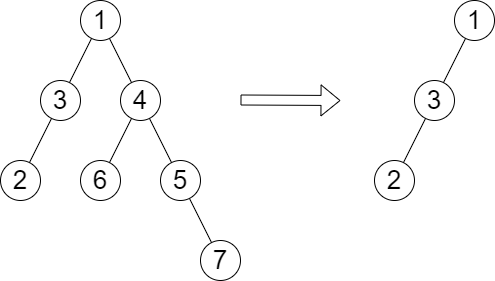
Input: root = [1,3,4,2,null,6,5,null,null,null,null,null,7], queries = [4]
Output: [2]
Explanation: The diagram above shows the tree after removing the subtree rooted at node with value 4.
The height of the tree is 2 (The path 1 -> 3 -> 2).

Example 2:

Input: root = [5,8,9,2,1,3,7,4,6], queries = [3,2,4,8]
Output: [3,2,3,2]
Explanation: We have the following queries:
- Removing the subtree rooted at node with value 3. The height of the tree becomes 3 (The path 5 -> 8 -> 2 -> 4).
- Removing the subtree rooted at node with value 2. The height of the tree becomes 2 (The path 5 -> 8 -> 1).
- Removing the subtree rooted at node with value 4. The height of the tree becomes 3 (The path 5 -> 8 -> 2 -> 6).
- Removing the subtree rooted at node with value 8. The height of the tree becomes 2 (The path 5 -> 9 -> 3).

Constraints:

• The number of nodes in the tree is n.
• 2 <= n <= 105
• 1 <= Node.val <= n
• All the values in the tree are unique.
• m == queries.length
• 1 <= m <= min(n, 104)
• 1 <= queries[i] <= n
• queries[i] != root.val

Approach 01:

class Solution {
public:
    vector<int> treeQueries(TreeNode* root, vector<int>& queries) {
        vector<int> result;

        calculateHeights(root, 0, 0);

        for (const int query : queries){
            result.push_back(nodeToMaxHeight[query]);
        }

        return result;
    }

private:
    // nodeToMaxHeight[val] stores the maximum height of the tree without the
    // node with `val`
    unordered_map<int, int> nodeToMaxHeight;
    // nodeToHeight[val] stores the height of the node with `val`
    unordered_map<int, int> nodeToHeight;

    // Helper function to calculate the height of a node
    int getHeight(TreeNode* root) {
        if (root == nullptr)
            return 0;
        if (const auto it = nodeToHeight.find(root->val);
            it != nodeToHeight.cend())
            return it->second;
        return nodeToHeight[root->val] = (1 + max(getHeight(root->left), getHeight(root->right)));
    }

    // maxHeight: the maximum height excluding the current node `root`
    void calculateHeights(TreeNode* root, int currentDepth, int maxHeight) {
        if (root == nullptr)
            return;
        nodeToMaxHeight[root->val] = maxHeight;
        calculateHeights(root->left, currentDepth + 1, max(maxHeight, currentDepth + getHeight(root->right)));
        calculateHeights(root->right, currentDepth + 1, max(maxHeight, currentDepth + getHeight(root->left)));
    }
};

class Solution:
    def treeQueries(self, root: 'TreeNode', queries: list[int]) -> list[int]:
        result = []
        
        # Calculate heights for all nodes
        self.calculateHeights(root, 0, 0)

        # Retrieve the maximum height for each query
        for query in queries:
            result.append(self.nodeToMaxHeight[query])

        return result

    def __init__(self):
        # nodeToMaxHeight[nodeValue] stores the maximum height excluding the node with `nodeValue`
        self.nodeToMaxHeight = {}
        # nodeToHeight[nodeValue] stores the height of the node with `nodeValue`
        self.nodeToHeight = {}

    # Helper function to get the height of a node
    def getHeight(self, root: 'TreeNode') -> int:
        if not root:
            return 0
        if root.val in self.nodeToHeight:
            return self.nodeToHeight[root.val]
        self.nodeToHeight[root.val] = 1 + max(self.getHeight(root.left), self.getHeight(root.right))
        return self.nodeToHeight[root.val]

    # Recursive function to calculate heights and update maxHeight without the current node
    def calculateHeights(self, root: 'TreeNode', currentDepth: int, maxHeight: int):
        if not root:
            return
        self.nodeToMaxHeight[root.val] = maxHeight
        self.calculateHeights(root.left, currentDepth + 1, max(maxHeight, currentDepth + self.getHeight(root.right)))
        self.calculateHeights(root.right, currentDepth + 1, max(maxHeight, currentDepth + self.getHeight(root.left)))

Time Complexity

• Calculating Heights:

  The function getHeight is called for each node of the tree to calculate its height. Each node is visited once, so the time complexity of this operation is \(O(n)\), where n is the number of nodes in the tree.

• Calculating Maximum Heights:

  The function calculateHeights also visits each node once to compute the maximum height excluding the current node. Since each node is visited once, this step also takes \(O(n)\) time.

• Processing Queries:

  For each query, retrieving the precomputed height from the nodeToMaxHeight map is an \(O(1)\) operation. If there are \(q\) queries, this step takes \(O(q)\).

• Overall Time Complexity:

  The total time complexity is \(O(n + q)\), where n is the number of nodes in the tree, and q is the number of queries.

Space Complexity

• Space for Height Maps:

  Two unordered maps, nodeToMaxHeight and nodeToHeight, store values for each node. In the worst case, they each store \(n\) entries, leading to \(O(n)\) space usage.

• Recursion Stack:

  The depth of recursion depends on the height of the tree. In the worst case (unbalanced tree), the recursion stack can take up to \(O(n)\) space.

• Other Variables:

  The result vector and query vector take \(O(q)\) space, where \(q\) is the number of queries.

• Overall Space Complexity:

  The total space complexity is \(O(n + q)\), where n is the number of nodes in the tree, and q is the number of queries.