2577. Minimum Time to Visit a Cell In a Grid

You are given a m x n matrix grid consisting of non-negative integers where grid[row][col] represents the minimum time required to be able to visit the cell (row, col), which means you can visit the cell (row, col) only when the time you visit it is greater than or equal to grid[row][col].

You are standing in the top-left cell of the matrix in the 0th second, and you must move to any adjacent cell in the four directions: up, down, left, and right. Each move you make takes 1 second.

Return the minimum time required in which you can visit the bottom-right cell of the matrix. If you cannot visit the bottom-right cell, then return -1.

Example 1:

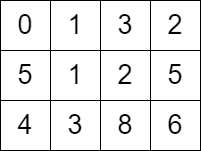
Input: grid = [[0,1,3,2],[5,1,2,5],[4,3,8,6]]
Output: 7
Explanation: One of the paths that we can take is the following:
- at t = 0, we are on the cell (0,0).
- at t = 1, we move to the cell (0,1). It is possible because grid[0][1] <= 1.
- at t = 2, we move to the cell (1,1). It is possible because grid[1][1] <= 2.
- at t = 3, we move to the cell (1,2). It is possible because grid[1][2] <= 3.
- at t = 4, we move to the cell (1,1). It is possible because grid[1][1] <= 4.
- at t = 5, we move to the cell (1,2). It is possible because grid[1][2] <= 5.
- at t = 6, we move to the cell (1,3). It is possible because grid[1][3] <= 6.
- at t = 7, we move to the cell (2,3). It is possible because grid[2][3] <= 7.
The final time is 7. It can be shown that it is the minimum time possible.

Example 2:

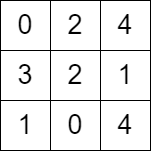
Input: grid = [[0,2,4],[3,2,1],[1,0,4]]
Output: -1
Explanation: There is no path from the top left to the bottom-right cell.

Constraints:

• m == grid.length
• n == grid[i].length
• 2 <= m, n <= 1000
• 4 <= m * n <= 105
• 0 <= grid[i][j] <= 105
• grid[0][0] == 0

Approach 01:

class Solution {
 public:
  int minimumTime(vector<vector<int>>& grid) {
    if (grid[0][1] > 1 && grid[1][0] > 1)
      return -1;

    constexpr int directions[4][2] = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
    const int rows = grid.size();
    const int cols = grid[0].size();
    using Cell = tuple<int, int, int>;  // (currentTime, row, col)
    priority_queue<Cell, vector<Cell>, greater<>> minHeap;
    vector<vector<bool>> visited(rows, vector<bool>(cols));

    minHeap.emplace(0, 0, 0);
    visited[0][0] = true;

    while (!minHeap.empty()) {
      const auto [currentTime, row, col] = minHeap.top();
      minHeap.pop();
      if (row == rows - 1 && col == cols - 1)
        return currentTime;
      for (const auto& [dx, dy] : directions) {
        const int newRow = row + dx;
        const int newCol = col + dy;
        if (newRow < 0 || newRow == rows || newCol < 0 || newCol == cols)
          continue;
        if (visited[newRow][newCol])
          continue;
        const int waitTime = (grid[newRow][newCol] - currentTime) % 2 == 0 ? 1 : 0;
        const int nextTime = max(currentTime + 1, grid[newRow][newCol] + waitTime);
        minHeap.emplace(nextTime, newRow, newCol);
        visited[newRow][newCol] = true;
      }
    }

    throw;
  }
};

from heapq import heappush, heappop

class Solution:
    def minimumTime(self, grid: list[list[int]]) -> int:
        if grid[0][1] > 1 and grid[1][0] > 1:
            return -1

        directions = [(0, 1), (1, 0), (0, -1), (-1, 0)]
        rows, cols = len(grid), len(grid[0])
        minHeap = [(0, 0, 0)]  # (currentTime, row, col)
        visited = [[False] * cols for _ in range(rows)]
        visited[0][0] = True

        while minHeap:
            currentTime, row, col = heappop(minHeap)
            if row == rows - 1 and col == cols - 1:
                return currentTime
            for dx, dy in directions:
                newRow, newCol = row + dx, col + dy
                if newRow < 0 or newRow == rows or newCol < 0 or newCol == cols:
                    continue
                if visited[newRow][newCol]:
                    continue
                waitTime = (grid[newRow][newCol] - currentTime) % 2 == 0
                nextTime = max(currentTime + 1, grid[newRow][newCol] + (1 if waitTime else 0))
                heappush(minHeap, (nextTime, newRow, newCol))
                visited[newRow][newCol] = True

        raise Exception("Path to the destination was not found.")

Time Complexity

• Heap operations:

  Each cell in the grid can be visited at most once. For each cell, the operation of pushing or updating in the min-heap takes \(O(\log(k))\), where \(k\) is the number of elements in the heap. Since there are \(m \times n\) cells, the total time complexity of the heap operations is \(O((m \times n) \log(m \times n))\).

• Neighbor traversal:

  For each cell, up to 4 neighbors are checked. This step is linear in the number of cells, contributing \(O(m \times n)\).

• Overall Time Complexity:

  The overall time complexity is \(O((m \times n) \log(m \times n))\), dominated by the heap operations.

Space Complexity

• Min-Heap:

  The heap can contain up to \(m \times n\) elements in the worst case, requiring \(O(m \times n)\) space.

• Visited Matrix:

  The visited matrix visited has dimensions \(m \times n\), consuming \(O(m \times n)\) space.

• Overall Space Complexity:

  The overall space complexity is \(O(m \times n)\), where \(m\) is the number of rows and \(n\) is the number of columns.