2641. Cousins in Binary Tree II

Given the root of a binary tree, replace the value of each node in the tree with the sum of all its cousins’ values.

Two nodes of a binary tree are cousins if they have the same depth with different parents.

Return the root of the modified tree.

Note that the depth of a node is the number of edges in the path from the root node to it.

Example 1:

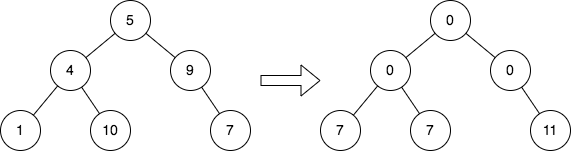
Input: root = [5,4,9,1,10,null,7]
Output: [0,0,0,7,7,null,11]
Explanation: The diagram above shows the initial binary tree and the binary tree after changing the value of each node.
- Node with value 5 does not have any cousins so its sum is 0.
- Node with value 4 does not have any cousins so its sum is 0.
- Node with value 9 does not have any cousins so its sum is 0.
- Node with value 1 has a cousin with value 7 so its sum is 7.
- Node with value 10 has a cousin with value 7 so its sum is 7.
- Node with value 7 has cousins with values 1 and 10 so its sum is 11.

Example 2:

Input: root = [3,1,2]
Output: [0,0,0]
Explanation: The diagram above shows the initial binary tree and the binary tree after changing the value of each node.
- Node with value 3 does not have any cousins so its sum is 0.
- Node with value 1 does not have any cousins so its sum is 0.
- Node with value 2 does not have any cousins so its sum is 0.

Constraints:

• The number of nodes in the tree is in the range [1, 105].
• 1 <= Node.val <= 104

Approach 01:

class Solution {
public:
    TreeNode* replaceValueInTree(TreeNode* root) {
        root->val = 0;
        queue<TreeNode*> nodeQueue;
        nodeQueue.push(root);

        while (!nodeQueue.empty()) {
            int levelSize = nodeQueue.size(), levelSum = 0;
            vector<TreeNode*> nodesAtCurrentLevel;

            // Process each node at the current level
            while (levelSize--) {
                TreeNode* currentNode = nodeQueue.front();
                nodeQueue.pop();
                nodesAtCurrentLevel.push_back(currentNode);

                if (currentNode->left) {
                    nodeQueue.push(currentNode->left);
                    levelSum += currentNode->left->val;
                }
                if (currentNode->right) {
                    nodeQueue.push(currentNode->right);
                    levelSum += currentNode->right->val;
                }
            }

            // Replace node values based on cousin sum
            for (auto currentNode : nodesAtCurrentLevel) {
                int cousinSum = levelSum;
                if (currentNode->left)
                    cousinSum -= currentNode->left->val;
                if (currentNode->right)
                    cousinSum -= currentNode->right->val;
                if (currentNode->left)
                    currentNode->left->val = cousinSum;
                if (currentNode->right)
                    currentNode->right->val = cousinSum;
            }
        }
        return root;
    }
};

from collections import deque

class Solution:
    def replaceValueInTree(self, root: TreeNode) -> TreeNode:
        root.val = 0
        nodeQueue = deque([root])

        while nodeQueue:
            levelSize = len(nodeQueue)
            levelSum = 0
            nodesAtCurrentLevel = []

            # Process each node at the current level
            for _ in range(levelSize):
                currentNode = nodeQueue.popleft()
                nodesAtCurrentLevel.append(currentNode)

                if currentNode.left:
                    nodeQueue.append(currentNode.left)
                    levelSum += currentNode.left.val
                if currentNode.right:
                    nodeQueue.append(currentNode.right)
                    levelSum += currentNode.right.val

            # Replace node values based on cousin sum
            for currentNode in nodesAtCurrentLevel:
                cousinSum = levelSum
                if currentNode.left:
                    cousinSum -= currentNode.left.val
                if currentNode.right:
                    cousinSum -= currentNode.right.val
                if currentNode.left:
                    currentNode.left.val = cousinSum
                if currentNode.right:
                    currentNode.right.val = cousinSum

        return root

Time Complexity

• Level-order Traversal (BFS):

  We perform a breadth-first search (BFS) to traverse each level of the tree. During each level, we process all nodes and compute the sum of their children’s values. Each node is visited exactly once, and for each node, we perform constant-time operations (updating the value, summing children). Therefore, the time complexity is \(O(n)\), where n is the number of nodes in the tree.

• Overall Time Complexity:

  The overall time complexity is \(O(n)\), where n is the total number of nodes.

Space Complexity

• Queue Storage:

  The space required to store the queue is \(O(w)\), where w is the maximum width of the tree. In the worst case, this could be \(O(n)\) (if the tree is balanced, the maximum number of nodes at a level is about half the total number of nodes).

• Temporary Storage for Nodes at Each Level:

  We store the nodes of the current level in the vector nodesAtCurrentLevel. This also uses space proportional to the width of the tree, which is \(O(w)\).

• Overall Space Complexity:

  The overall space complexity is \(O(n)\) in the worst case, due to the storage needed for the BFS queue and the level vector.