2658. Maximum Number of Fish in a Grid

You are given a 0-indexed 2D matrix grid of size m x n, where (r, c) represents:

• A land cell if grid[r][c] = 0, or
• A water cell containing grid[r][c] fish, if grid[r][c] > 0.

A fisher can start at any water cell (r, c) and can do the following operations any number of times:

• Catch all the fish at cell (r, c), or
• Move to any adjacent water cell.

Return the maximum number of fish the fisher can catch if he chooses his starting cell optimally, or 0 if no water cell exists.

An adjacent cell of the cell (r, c), is one of the cells (r, c + 1), (r, c - 1), (r + 1, c) or (r - 1, c) if it exists.

Example 1:

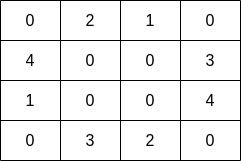
Input: grid = [[0,2,1,0],[4,0,0,3],[1,0,0,4],[0,3,2,0]]
Output: 7
Explanation: The fisher can start at cell (1,3) and collect 3 fish, then move to cell (2,3) and collect 4 fish.

Example 2:

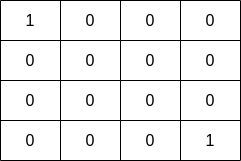
Input: grid = [[1,0,0,0],[0,0,0,0],[0,0,0,0],[0,0,0,1]]
Output: 1
Explanation: The fisher can start at cells (0,0) or (3,3) and collect a single fish.

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 10
• 0 <= grid[i][j] <= 10

Approach 01:

#include <vector>
#include <algorithm>
using namespace std;

class Solution {
 public:
  int findMaxFish(vector<vector<int>>& grid) {
    int maxFish = 0;  // Maximum fish that can be collected

    for (int row = 0; row < grid.size(); ++row) {
      for (int col = 0; col < grid[0].size(); ++col) {
        if (grid[row][col] > 0) {
          maxFish = max(maxFish, performDFS(grid, row, col));
        }
      }
    }

    return maxFish;
  }

 private:
  int performDFS(vector<vector<int>>& grid, int row, int col) {
    // Check for out-of-bounds or water cell (value 0)
    if (row < 0 || row >= grid.size() || col < 0 || col >= grid[0].size() || grid[row][col] == 0) {
      return 0;
    }

    int fishCaught = grid[row][col];  // Fish caught at this cell
    grid[row][col] = 0;  // Mark the cell as visited by setting it to 0

    // Recursively collect fish in all four directions
    return fishCaught + 
           performDFS(grid, row + 1, col) +
           performDFS(grid, row - 1, col) +
           performDFS(grid, row, col + 1) +
           performDFS(grid, row, col - 1);
  }
};

class Solution:
    def findMaxFish(self, grid: list[list[int]]) -> int:
        maxFish = 0  # Maximum fish that can be collected

        for row in range(len(grid)):
            for col in range(len(grid[0])):
                if grid[row][col] > 0:
                    maxFish = max(maxFish, self.performDFS(grid, row, col))

        return maxFish

    def performDFS(self, grid: list[list[int]], row: int, col: int) -> int:
        # Check for out-of-bounds or water cell (value 0)
        if row < 0 or row >= len(grid) or col < 0 or col >= len(grid[0]) or grid[row][col] == 0:
            return 0

        fishCaught = grid[row][col]  # Fish caught at this cell
        grid[row][col] = 0  # Mark the cell as visited by setting it to 0

        # Recursively collect fish in all four directions
        return fishCaught + \
               self.performDFS(grid, row + 1, col) + \
               self.performDFS(grid, row - 1, col) + \
               self.performDFS(grid, row, col + 1) + \
               self.performDFS(grid, row, col - 1)

Time Complexity:

• DFS Traversal:

  In the worst case, every cell in the grid is visited once during the DFS traversal. Each cell is marked as visited and processed, which takes \( O(1) \) time per cell. Therefore, the DFS traversal takes \( O(m \cdot n) \), where \( m \) is the number of rows and \( n \) is the number of columns in the grid.

• Outer Loop:

  The double loop iterates through all cells in the grid, which also takes \( O(m \cdot n) \).

• Overall Time Complexity:

  The total time complexity is \( O(m \cdot n) \), as each cell is visited at most once during DFS.

Space Complexity:

• Recursion Stack:

  DFS uses a recursion stack to store the function calls for neighboring cells. In the worst case, the maximum depth of the recursion is equal to the total number of cells in a connected component, which is \( O(m \cdot n) \) in the worst-case scenario where all cells are part of a single connected component.

• Grid Storage:

  The input grid is modified in place, so no additional space is required for storing visited cells.

• Overall Space Complexity:

  The overall space complexity is \( O(m \cdot n) \), dominated by the recursion stack.