You are given an undirected weighted connected graph containing n nodes labeled from 0 to n - 1, and an integer array edges where edges[i] = [ai, bi, wi] indicates that there is an edge between nodes ai and bi with weight wi.
Some edges have a weight of -1 (wi = -1), while others have a positive weight (wi > 0).
Your task is to modify all edges with a weight of -1 by assigning them positive integer values in the range [1, 2 * 109] so that the shortest distance between the nodes source and destination becomes equal to an integer target. If there are multiple modifications that make the shortest distance between source and destination equal to target, any of them will be considered correct.
Return an array containing all edges (even unmodified ones) in any order if it is possible to make the shortest distance from source to destination equal to target, or an empty array if it’s impossible.
Note: You are not allowed to modify the weights of edges with initial positive weights.
Example 1:
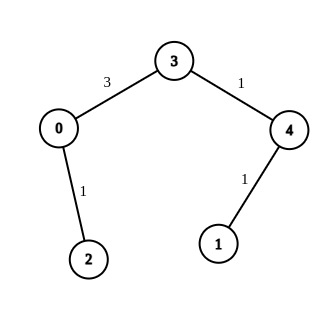
Input: n = 5, edges = [[4,1,-1],[2,0,-1],[0,3,-1],[4,3,-1]], source = 0, destination = 1, target = 5 Output: [[4,1,1],[2,0,1],[0,3,3],[4,3,1]] Explanation: The graph above shows a possible modification to the edges, making the distance from 0 to 1 equal to 5.
Example 2:
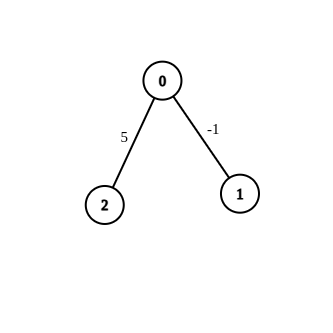
Input: n = 3, edges = [[0,1,-1],[0,2,5]], source = 0, destination = 2, target = 6 Output: [] Explanation: The graph above contains the initial edges. It is not possible to make the distance from 0 to 2 equal to 6 by modifying the edge with weight -1. So, an empty array is returned.
Example 3:
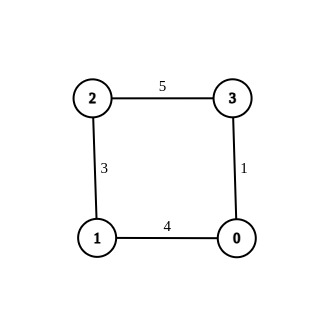
Input: n = 4, edges = [[1,0,4],[1,2,3],[2,3,5],[0,3,-1]], source = 0, destination = 2, target = 6 Output: [[1,0,4],[1,2,3],[2,3,5],[0,3,1]] Explanation: The graph above shows a modified graph having the shortest distance from 0 to 2 as 6.
Constraints:
1 <= n <= 1001 <= edges.length <= n * (n - 1) / 2edges[i].length == 30 <= ai, bi < nwi = -1or1 <= wi <= 107ai != bi0 <= source, destination < nsource != destination1 <= target <= 109- The graph is connected, and there are no self-loops or repeated edges
Approach 01:
-
C++
-
Python
class Solution {
public:
vector<vector<int>> modifiedGraphEdges(int numNodes, vector<vector<int>>& edges, int source, int destination, int target) {
constexpr int maxWeight = 2'000'000'000;
vector<vector<pair<int, int>>> adjacencyList(numNodes);
for (const vector<int>& edge : edges) {
const int startNode = edge[0];
const int endNode = edge[1];
const int weight = edge[2];
if (weight == -1)
continue;
adjacencyList[startNode].emplace_back(endNode, weight);
adjacencyList[endNode].emplace_back(startNode, weight);
}
int distanceToDestination = findShortestPath(adjacencyList, source, destination);
if (distanceToDestination < target)
return {};
if (distanceToDestination == target) {
// Change the weights of negative edges to an impossible value.
for (vector<int>& edge : edges)
if (edge[2] == -1)
edge[2] = maxWeight;
return edges;
}
for (int i = 0; i < edges.size(); ++i) {
const int startNode = edges[i][0];
const int endNode = edges[i][1];
int& weight = edges[i][2];
if (weight != -1)
continue;
weight = 1;
adjacencyList[startNode].emplace_back(endNode, 1);
adjacencyList[endNode].emplace_back(startNode, 1);
distanceToDestination = findShortestPath(adjacencyList, source, destination);
if (distanceToDestination <= target) {
weight += target - distanceToDestination;
// Change the weights of remaining negative edges to an impossible value.
for (int j = i + 1; j < edges.size(); ++j)
if (edges[j][2] == -1)
edges[j][2] = maxWeight;
return edges;
}
}
return {};
}
private:
int findShortestPath(const vector<vector<pair<int, int>>>& adjacencyList, int source, int destination) {
vector<int> minDistances(adjacencyList.size(), INT_MAX);
using DistanceNodePair = pair<int, int>; // (distance, node)
priority_queue<DistanceNodePair, vector<DistanceNodePair>, greater<>> minHeap;
minDistances[source] = 0;
minHeap.emplace(minDistances[source], source);
while (!minHeap.empty()) {
const auto [currentDistance, currentNode] = minHeap.top();
minHeap.pop();
if (currentDistance > minDistances[currentNode])
continue;
for (const auto& [adjacentNode, edgeWeight] : adjacencyList[currentNode]) {
if (currentDistance + edgeWeight < minDistances[adjacentNode]) {
minDistances[adjacentNode] = currentDistance + edgeWeight;
minHeap.emplace(minDistances[adjacentNode], adjacentNode);
}
}
}
return minDistances[destination];
}
};
import heapq
from typing import List, Tuple
class Solution:
def modifiedGraphEdges(self, numNodes: int, edges: List[List[int]], source: int, destination: int, target: int) -> List[List[int]]:
maxWeight = 2_000_000_000
adjacencyList = [[] for _ in range(numNodes)]
# Build the adjacency list
for edge in edges:
startNode, endNode, weight = edge
if weight != -1: # Only add positive-weight edges to adjacency list
adjacencyList[startNode].append((endNode, weight))
adjacencyList[endNode].append((startNode, weight))
# Calculate the shortest path from source to destination
distanceToDestination = self.findShortestPath(adjacencyList, source, destination)
if distanceToDestination < target:
return []
if distanceToDestination == target:
# Change the weights of negative edges to an impossible value.
for edge in edges:
if edge[2] == -1:
edge[2] = maxWeight
return edges
# Adjust negative edges' weights to achieve the desired shortest path
for i in range(len(edges)):
startNode, endNode = edges[i][0], edges[i][1]
weight = edges[i][2]
if weight != -1:
continue
# Set weight to 1 temporarily to try achieving the target distance
edges[i][2] = 1
adjacencyList[startNode].append((endNode, 1))
adjacencyList[endNode].append((startNode, 1))
distanceToDestination = self.findShortestPath(adjacencyList, source, destination)
if distanceToDestination <= target:
edges[i][2] += (target - distanceToDestination) # Adjust weight to make the total distance equal to the target
# Change the weights of remaining negative edges to an impossible value.
for j in range(i + 1, len(edges)):
if edges[j][2] == -1:
edges[j][2] = maxWeight
return edges
return []
def findShortestPath(self, adjacencyList: List[List[Tuple[int, int]]], source: int, destination: int) -> int:
# Initialize the minimum distances array with infinity
minDistances = [float('inf')] * len(adjacencyList)
minHeap = [] # Priority queue to store (distance, node) pairs
# Set the distance to the source as 0 and push to the priority queue
minDistances[source] = 0
heapq.heappush(minHeap, (0, source))
while minHeap:
currentDistance, currentNode = heapq.heappop(minHeap)
# Skip processing if a shorter path to currentNode is already found
if currentDistance > minDistances[currentNode]:
continue
# Traverse all adjacent nodes
for adjacentNode, edgeWeight in adjacencyList[currentNode]:
# If a shorter path is found
if currentDistance + edgeWeight < minDistances[adjacentNode]:
minDistances[adjacentNode] = currentDistance + edgeWeight
heapq.heappush(minHeap, (minDistances[adjacentNode], adjacentNode))
return minDistances[destination]
Time Complexity
- Initial Shortest Path Calculation:
The algorithm calculates the shortest path from the
sourceto thedestinationusing Dijkstra’s algorithm. The time complexity of Dijkstra’s algorithm with a priority queue is \( O((E + V) \log V) \), where \( E \) is the number of edges and \( V \) is the number of nodes. - Edge Modification and Recalculation:
The algorithm iterates over all edges and potentially recalculates the shortest path for each edge where the weight is initially -1. In the worst case, it performs up to \( E \) recalculations of the shortest path, each taking \( O((E + V) \log V) \) time.
Therefore, the time complexity for this part is \( O(E \cdot (E + V) \log V) \).
- Overall Time Complexity:
The overall time complexity is \( O(E \cdot (E + V) \log V) \), combining the initial shortest path calculation and edge modifications with recalculations.
Space Complexity
- Adjacency List:
The adjacency list requires \( O(E) \) space to store all edges in the graph.
- Distance Array:
The
minDistancesarray requires \( O(V) \) space to store the shortest distances from the source node to all other nodes. - Priority Queue:
The priority queue used in Dijkstra’s algorithm can contain up to \( V \) nodes, requiring \( O(V) \) space.
- Overall Space Complexity:
The overall space complexity is \( O(E + V) \), considering the space for the adjacency list, distance array, and priority queue.