2751. Robot Collisions

There are n 1-indexed robots, each having a position on a line, health, and movement direction.

You are given 0-indexed integer arrays positions, healths, and a string directions (directions[i] is either ‘L’ for left or ‘R’ for right). All integers in positions are unique.

All robots start moving on the line simultaneously at the same speed in their given directions. If two robots ever share the same position while moving, they will collide.

If two robots collide, the robot with lower health is removed from the line, and the health of the other robot decreases by one. The surviving robot continues in the same direction it was going. If both robots have the same health, they are bothremoved from the line.

Your task is to determine the health of the robots that survive the collisions, in the same order that the robots were given,i.e. final heath of robot 1 (if survived), final health of robot 2 (if survived), and so on. If there are no survivors, return an empty array.

Return an array containing the health of the remaining robots (in the order they were given in the input), after no further collisions can occur.

Note: The positions may be unsorted.

Example 1:

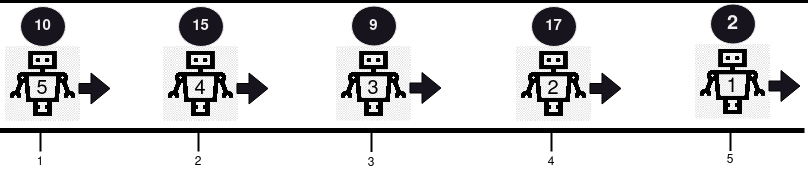
Input: positions = [5,4,3,2,1], healths = [2,17,9,15,10], directions = "RRRRR"
Output: [2,17,9,15,10]
Explanation: No collision occurs in this example, since all robots are moving in the same direction. So, the health of the robots in order from the first robot is returned, [2, 17, 9, 15, 10].

Example 2:

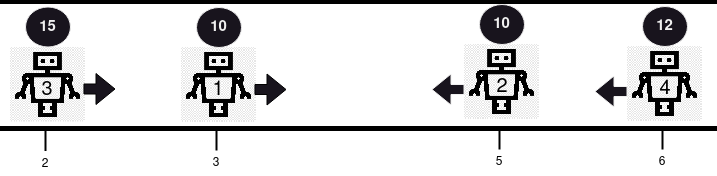
Input: positions = [3,5,2,6], healths = [10,10,15,12], directions = "RLRL"
Output: [14]
Explanation: There are 2 collisions in this example. Firstly, robot 1 and robot 2 will collide, and since both have the same health, they will be removed from the line. Next, robot 3 and robot 4 will collide and since robot 4's health is smaller, it gets removed, and robot 3's health becomes 15 - 1 = 14. Only robot 3 remains, so we return [14].

Example 3:

Input: positions = [1,2,5,6], healths = [10,10,11,11], directions = "RLRL"
Output: []
Explanation: Robot 1 and robot 2 will collide and since both have the same health, they are both removed. Robot 3 and 4 will collide and since both have the same health, they are both removed. So, we return an empty array, [].

Constraints:

• 1 <= positions.length == healths.length == directions.length == n <= 105
• 1 <= positions[i], healths[i] <= 109
• directions[i] == 'L' or directions[i] == 'R'
• All values in positions are distinct

Approach 01:

struct Robot {
    int index;
    int position;
    int health;
    char direction;
};

class Solution {
public:
    vector<int> survivedRobotsHealths(vector<int>& positions, vector<int>& healths, string directions) {
        vector<int> survivedHealths;
        vector<Robot> robots;
        vector<Robot> activeRobots; // Robots currently active in collision

        for (int i = 0; i < positions.size(); ++i) {
            robots.push_back(Robot{i, positions[i], healths[i], directions[i]});
        }

        ranges::sort(robots, [](const Robot& a, const Robot& b) {
            return a.position < b.position;
        });

        for (Robot& robot : robots) {
            if (robot.direction == 'R') {
                activeRobots.push_back(robot);
                continue;
            }
            // Collide with robots going right if any.
            while (!activeRobots.empty() &&
                   activeRobots.back().direction == 'R' && robot.health > 0) {
                if (activeRobots.back().health == robot.health) {
                    activeRobots.pop_back();
                    robot.health = 0;
                } else if (activeRobots.back().health < robot.health) {
                    activeRobots.pop_back();
                    robot.health -= 1;
                } else { // activeRobots.back().health > robot.health
                    activeRobots.back().health -= 1;
                    robot.health = 0;
                }
            }
            if (robot.health > 0) {
                activeRobots.push_back(robot);
            }
        }

        ranges::sort(activeRobots, [](const Robot& a, const Robot& b) {
            return a.index < b.index;
        });

        for (const Robot& robot : activeRobots) {
            survivedHealths.push_back(robot.health);
        }

        return survivedHealths;
    }
};

from typing import List

class Robot:
    def __init__(self, index: int, position: int, health: int, direction: str):
        self.index = index
        self.position = position
        self.health = health
        self.direction = direction

class Solution:
    def survivedRobotsHealths(self, positions: List[int], healths: List[int], directions: str) -> List[int]:
        survived_healths = []
        robots = []
        active_robots = []  # Robots currently active in collision

        for i in range(len(positions)):
            robots.append(Robot(i, positions[i], healths[i], directions[i]))

        robots.sort(key=lambda robot: robot.position)

        for robot in robots:
            if robot.direction == 'R':
                active_robots.append(robot)
                continue
            # Collide with robots going right if any.
            while active_robots and active_robots[-1].direction == 'R' and robot.health > 0:
                if active_robots[-1].health == robot.health:
                    active_robots.pop()
                    robot.health = 0
                elif active_robots[-1].health < robot.health:
                    active_robots.pop()
                    robot.health -= 1
                else:  # active_robots[-1].health > robot.health
                    active_robots[-1].health -= 1
                    robot.health = 0
            if robot.health > 0:
                active_robots.append(robot)

        active_robots.sort(key=lambda robot: robot.index)

        for robot in active_robots:
            survived_healths.append(robot.health)

        return survived_healths

Time Complexity

• Initialization and Sorting:

  Creating the robots vector and sorting it by position takes \( O(n \log n) \) time, where \( n \) is the number of robots.

• Processing Robots:

  The main loop iterates through each robot once, and the nested while loop may also iterate through each robot once in the worst case, resulting in \( O(n) \) time for this part.

• Final Sorting:

  Sorting the activeRobots by their original indices takes \( O(n \log n) \) time.

• Overall Time Complexity:

  The overall time complexity is dominated by the sorting operations, resulting in \( O(n \log n) \).

Space Complexity

• Auxiliary Space:

  The algorithm uses additional space for the robots and activeRobots vectors, which both store up to \( n \) robots, resulting in \( O(n) \) space usage.

• Overall Space Complexity:

  The overall space complexity is \( O(n) \).