There are n teams numbered from 0 to n - 1 in a tournament; each team is also a node in a DAG.
You are given the integer n and a 0-indexed 2D integer array edges of length m representing the DAG, where edges[i] = [ui, vi] indicates that there is a directed edge from team ui to team vi in the graph.
A directed edge from a to b in the graph means that team a is stronger than team b and team b is weaker than team a.
Team a will be the champion of the tournament if there is no team b that is stronger than team a.
Return the team that will be the champion of the tournament if there is a unique champion, otherwise, return -1.
Notes
- A cycle is a series of nodes
a1, a2, ..., an, an+1such that nodea1is the same node as nodean+1, the nodesa1, a2, ..., anare distinct, and there is a directed edge from the nodeaito nodeai+1for everyiin the range[1, n]. - A DAG is a directed graph that does not have any cycle.
Example 1:
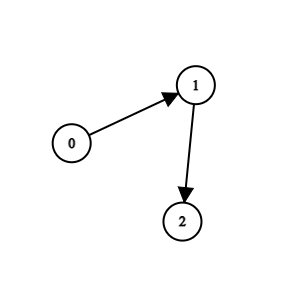
Input: n = 3, edges = [[0,1],[1,2]] Output: 0 Explanation: Team 1 is weaker than team 0. Team 2 is weaker than team 1. So the champion is team 0.
Example 2:
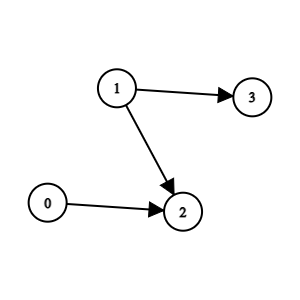
Input: n = 4, edges = [[0,2],[1,3],[1,2]] Output: -1 Explanation: Team 2 is weaker than team 0 and team 1. Team 3 is weaker than team 1. But team 1 and team 0 are not weaker than any other teams. So the answer is -1.
Constraints:
1 <= n <= 100m == edges.length0 <= m <= n * (n - 1) / 2edges[i].length == 20 <= edge[i][j] <= n - 1edges[i][0] != edges[i][1]- The input is generated such that if team
ais stronger than teamb, teambis not stronger than teama. - The input is generated such that if team
ais stronger than teamband teambis stronger than teamc, then teamais stronger than teamc.
Approach 01:
-
C++
-
Python
#include <vector>
using namespace std;
class Solution {
public:
int findChampion(int numNodes, vector<vector<int>>& edges) {
int potentialChampion = -1;
int zeroInDegreeCount = 0;
vector<int> inDegrees(numNodes);
// Calculate in-degrees for each node
for (const vector<int>& edge : edges) {
const int targetNode = edge[1];
++inDegrees[targetNode];
}
// Identify nodes with zero in-degree
for (int node = 0; node < numNodes; ++node) {
if (inDegrees[node] == 0) {
++zeroInDegreeCount;
potentialChampion = node;
}
}
// If more than one node has zero in-degree, no champion exists
return zeroInDegreeCount > 1 ? -1 : potentialChampion;
}
};
from typing import List
class Solution:
def findChampion(self, numNodes: int, edges: List[List[int]]) -> int:
potentialChampion = -1
zeroInDegreeCount = 0
inDegrees = [0] * numNodes
# Calculate in-degrees for each node
for edge in edges:
targetNode = edge[1]
inDegrees[targetNode] += 1
# Identify nodes with zero in-degree
for node in range(numNodes):
if inDegrees[node] == 0:
zeroInDegreeCount += 1
potentialChampion = node
# If more than one node has zero in-degree, no champion exists
return -1 if zeroInDegreeCount > 1 else potentialChampion
Time Complexity
- Calculating In-Degrees:
The loop iterates over all the edges to calculate the in-degrees of each node. This takes \( O(E) \), where \( E \) is the number of edges.
- Identifying Nodes with Zero In-Degree:
A single iteration over all the nodes is performed to find nodes with zero in-degree, which takes \( O(V) \), where \( V \) is the number of nodes.
- Overall Time Complexity:
\( O(V + E) \), as both steps are performed sequentially.
Space Complexity
- In-Degree Array:
The array `inDegrees` is used to store the in-degree of each node, which requires \( O(V) \) space.
- Auxiliary Variables:
Constant space is used for variables like `potentialChampion`, `zeroInDegreeCount`, and loop variables, requiring \( O(1) \) space.
- Overall Space Complexity:
\( O(V) \), dominated by the in-degree array.