There exist two undirected trees with n and m nodes, numbered from 0 to n - 1 and from 0 to m - 1, respectively. You are given two 2D integer arrays edges1 and edges2 of lengths n - 1 and m - 1, respectively, where edges1[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the first tree and edges2[i] = [ui, vi] indicates that there is an edge between nodes ui and vi in the second tree.
You must connect one node from the first tree with another node from the second tree with an edge.
Return the minimum possible diameter of the resulting tree.
The diameter of a tree is the length of the longest path between any two nodes in the tree.
Example 1:
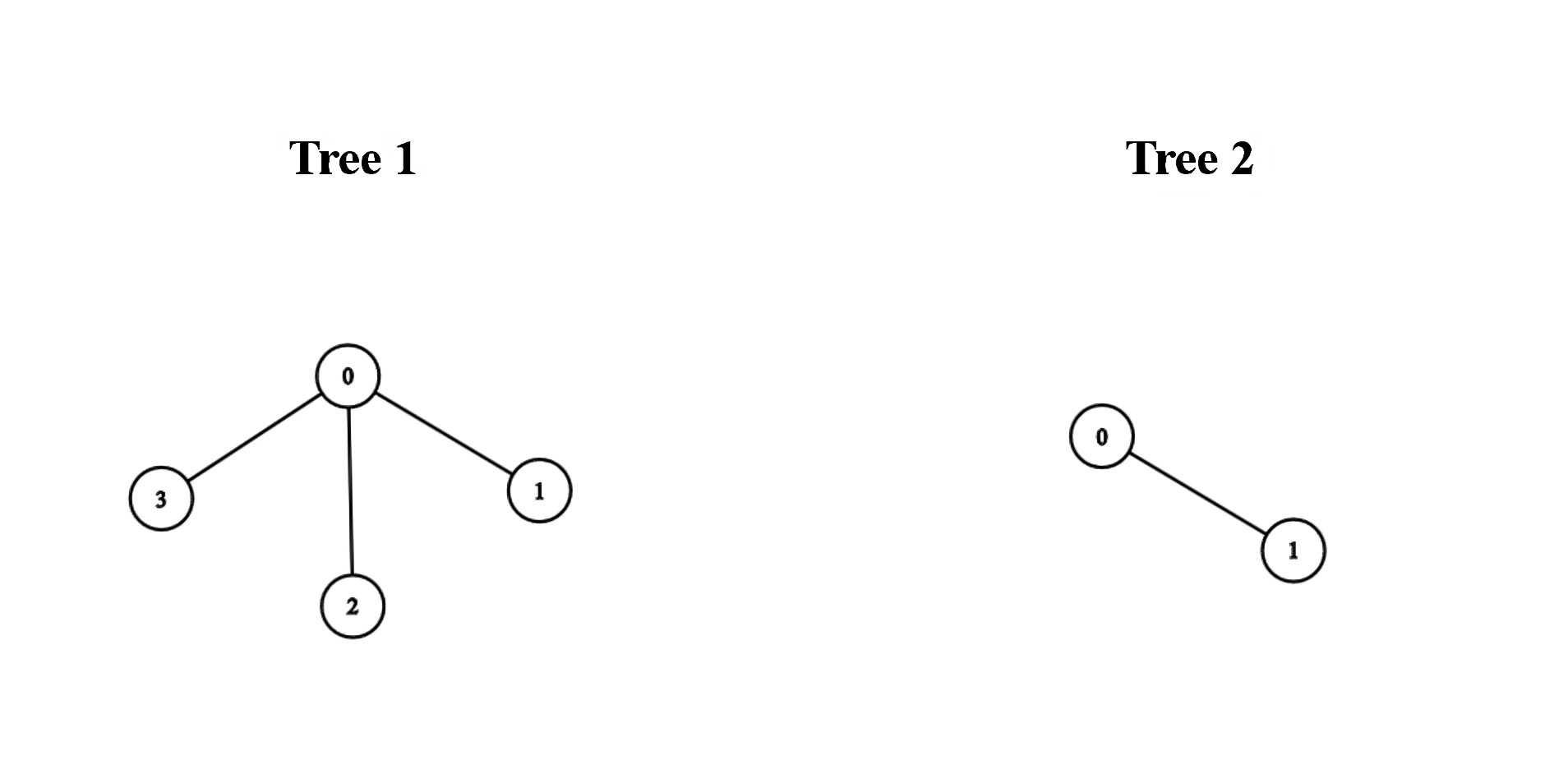
Input: edges1 = [[0,1],[0,2],[0,3]], edges2 = [[0,1]]
Output: 3
Explanation:
We can obtain a tree of diameter 3 by connecting node 0 from the first tree with any node from the second tree.
Example 2:
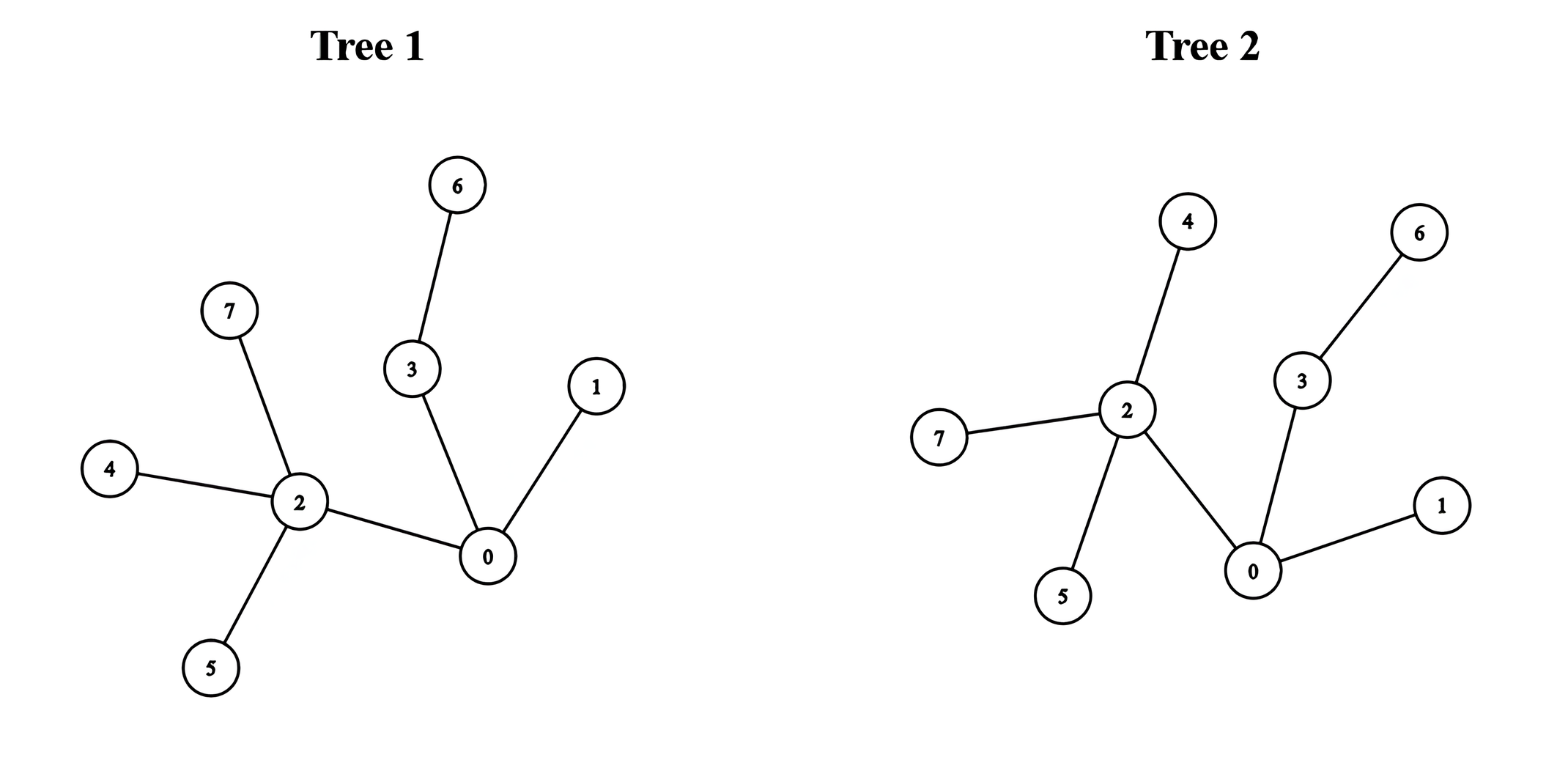
Input: edges1 = [[0,1],[0,2],[0,3],[2,4],[2,5],[3,6],[2,7]], edges2 = [[0,1],[0,2],[0,3],[2,4],[2,5],[3,6],[2,7]]
Output: 5
Explanation:
We can obtain a tree of diameter 5 by connecting node 0 from the first tree with node 0 from the second tree.
Constraints:
1 <= n, m <= 105edges1.length == n - 1edges2.length == m - 1edges1[i].length == edges2[i].length == 2edges1[i] = [ai, bi]0 <= ai, bi < nedges2[i] = [ui, vi]0 <= ui, vi < m- The input is generated such that
edges1andedges2represent valid trees.
Approach 01:
-
C++
-
Python
class Solution {
public:
int minimumDiameterAfterMerge(vector<vector<int>>& treeEdges1, vector<vector<int>>& treeEdges2) {
const int diameterTree1 = getDiameter(treeEdges1);
const int diameterTree2 = getDiameter(treeEdges2);
const int combinedDiameter = (diameterTree1 + 1) / 2 + (diameterTree2 + 1) / 2 + 1;
return max({diameterTree1, diameterTree2, combinedDiameter});
}
private:
int getDiameter(const vector<vector<int>>& treeEdges) {
const int totalNodes = treeEdges.size() + 1;
vector<vector<int>> adjacencyList(totalNodes);
for (const vector<int>& edge : treeEdges) {
const int node1 = edge[0];
const int node2 = edge[1];
adjacencyList[node1].push_back(node2);
adjacencyList[node2].push_back(node1);
}
int maxTreeDiameter = 0;
calculateMaxDepth(adjacencyList, 0, -1, maxTreeDiameter);
return maxTreeDiameter;
}
// Returns the maximum depth of the subtree rooted at currentNode.
int calculateMaxDepth(const vector<vector<int>>& adjacencyList, int currentNode, int parentNode, int& maxTreeDiameter) {
int maxSubtreeDepth1 = 0;
int maxSubtreeDepth2 = 0;
for (const int neighbor : adjacencyList[currentNode]) {
if (neighbor == parentNode)
continue;
const int currentSubtreeDepth = calculateMaxDepth(adjacencyList, neighbor, currentNode, maxTreeDiameter);
if (currentSubtreeDepth > maxSubtreeDepth1) {
maxSubtreeDepth2 = maxSubtreeDepth1;
maxSubtreeDepth1 = currentSubtreeDepth;
} else if (currentSubtreeDepth > maxSubtreeDepth2) {
maxSubtreeDepth2 = currentSubtreeDepth;
}
}
maxTreeDiameter = max(maxTreeDiameter, maxSubtreeDepth1 + maxSubtreeDepth2);
return 1 + maxSubtreeDepth1;
}
};
class Solution:
def minimumDiameterAfterMerge(self, treeEdges1: list[list[int]], treeEdges2: list[list[int]]) -> int:
diameterTree1 = self.getDiameter(treeEdges1)
diameterTree2 = self.getDiameter(treeEdges2)
combinedDiameter = (diameterTree1 + 1) // 2 + (diameterTree2 + 1) // 2 + 1
return max(diameterTree1, diameterTree2, combinedDiameter)
def getDiameter(self, treeEdges: list[list[int]]) -> int:
totalNodes = len(treeEdges) + 1
adjacencyList = [[] for _ in range(totalNodes)]
for edge in treeEdges:
node1, node2 = edge
adjacencyList[node1].append(node2)
adjacencyList[node2].append(node1)
maxTreeDiameter = [0] # Using a list to mimic pass-by-reference behavior
self.calculateMaxDepth(adjacencyList, 0, -1, maxTreeDiameter)
return maxTreeDiameter[0]
def calculateMaxDepth(self, adjacencyList: list[list[int]], currentNode: int, parentNode: int, maxTreeDiameter: list[int]) -> int:
maxSubtreeDepth1 = 0
maxSubtreeDepth2 = 0
for neighbor in adjacencyList[currentNode]:
if neighbor == parentNode:
continue
currentSubtreeDepth = self.calculateMaxDepth(adjacencyList, neighbor, currentNode, maxTreeDiameter)
if currentSubtreeDepth > maxSubtreeDepth1:
maxSubtreeDepth2 = maxSubtreeDepth1
maxSubtreeDepth1 = currentSubtreeDepth
elif currentSubtreeDepth > maxSubtreeDepth2:
maxSubtreeDepth2 = currentSubtreeDepth
maxTreeDiameter[0] = max(maxTreeDiameter[0], maxSubtreeDepth1 + maxSubtreeDepth2)
return 1 + maxSubtreeDepth1
Time Complexity
- Building the Adjacency List:
- The adjacency list is constructed by iterating through all edges of the tree. If the tree has \( n \) nodes, the number of edges is \( n – 1 \).
- Time complexity for this step is \( O(n) \).
- Depth-First Search (DFS):
- A DFS is performed to calculate the diameter of each tree. Since the algorithm visits each node and edge once, the time complexity for one DFS is \( O(n) \).
- Processing Two Trees:
- Since the function processes two trees, the total time complexity is:
\( O(n_1 + n_2) \), where \( n_1 \) and \( n_2 \) are the number of nodes in the two trees.
- Since the function processes two trees, the total time complexity is:
- Overall Time Complexity:
The overall time complexity is:
\( O(n_1 + n_2) \).
Space Complexity
- Adjacency List Storage:
- The adjacency list for each tree requires \( O(n) \) space, where \( n \) is the number of nodes in the tree.
- Recursion Stack:
- The recursion stack during DFS can grow up to \( O(h) \), where \( h \) is the height of the tree. In the worst case, \( h = n \), making the space complexity for the recursion stack \( O(n) \).
- Auxiliary Variables:
- Additional variables like
maxSubtreeDepth1,maxSubtreeDepth2, and others use \( O(1) \) space.
- Additional variables like
- Overall Space Complexity:
The total space complexity is:
\( O(n_1 + n_2) \), including adjacency lists and recursion stacks for both trees.