684. Redundant Connection

In this problem, a tree is an undirected graph that is connected and has no cycles.

You are given a graph that started as a tree with n nodes labeled from 1 to n, with one additional edge added. The added edge has two different vertices chosen from 1 to n, and was not an edge that already existed. The graph is represented as an array edges of length n where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the graph.

Return an edge that can be removed so that the resulting graph is a tree of n nodes. If there are multiple answers, return the answer that occurs last in the input.

Example 1:

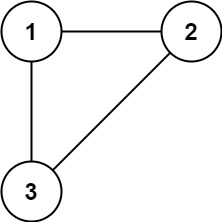
Input: edges = [[1,2],[1,3],[2,3]]
Output: [2,3]

Example 2:

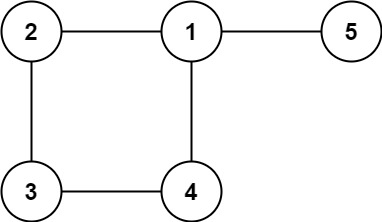
Input: edges = [[1,2],[2,3],[3,4],[1,4],[1,5]]
Output: [1,4]

Constraints:

• n == edges.length
• 3 <= n <= 1000
• edges[i].length == 2
• 1 <= ai < bi <= edges.length
• ai != bi
• There are no repeated edges.
• The given graph is connected.

Approach 01:

#include <vector>
#include <numeric>
using namespace std;

class UnionFind {
 public:
  UnionFind(int size) : parent(size), rank(size) {
    iota(parent.begin(), parent.end(), 0); // Initialize each node as its own parent
  }

  bool unionByRank(int node1, int node2) {
    int root1 = find(node1);
    int root2 = find(node2);

    if (root1 == root2)  
      return false;  // Cycle detected

    // Union by rank
    if (rank[root1] < rank[root2]) {
      parent[root1] = root2;
    } else if (rank[root1] > rank[root2]) {
      parent[root2] = root1;
    } else {
      parent[root1] = root2;
      ++rank[root2];
    }

    return true;
  }

 private:
  vector<int> parent;
  vector<int> rank;

  int find(int node) {
    return parent[node] == node ? node : parent[node] = find(parent[node]);  // Path compression
  }
};

class Solution {
 public:
  vector<int> findRedundantConnection(vector<vector<int>>& edges) {
    UnionFind unionFind(edges.size() + 1);

    for (const vector<int>& edge : edges) {
      int node1 = edge[0];
      int node2 = edge[1];

      if (!unionFind.unionByRank(node1, node2))  // If adding this edge forms a cycle
        return edge;
    }

    throw;  // This should never be reached
  }
};

class UnionFind:
    def __init__(self, size: int):
        self.parent = list(range(size))  # Initialize each node as its own parent
        self.rank = [0] * size  # Rank for union by rank optimization

    def unionByRank(self, node1: int, node2: int) -> bool:
        root1 = self.find(node1)
        root2 = self.find(node2)

        if root1 == root2:
            return False  # Cycle detected

        # Union by rank
        if self.rank[root1] < self.rank[root2]:
            self.parent[root1] = root2
        elif self.rank[root1] > self.rank[root2]:
            self.parent[root2] = root1
        else:
            self.parent[root1] = root2
            self.rank[root2] += 1

        return True

    def find(self, node: int) -> int:
        if self.parent[node] != node:
            self.parent[node] = self.find(self.parent[node])  # Path compression
        return self.parent[node]


class Solution:
    def findRedundantConnection(self, edges: list[list[int]]) -> list[int]:
        unionFind = UnionFind(len(edges) + 1)

        for node1, node2 in edges:
            if not unionFind.unionByRank(node1, node2):  # If adding this edge forms a cycle
                return [node1, node2]

        raise Exception("No redundant connection found")

Time Complexity:

• Find Operation:

  Using path compression, the find operation runs in nearly constant time, i.e., \( O(\alpha(n)) \), where \( \alpha(n) \) is the inverse Ackermann function.

• Union Operation:

  Union by rank ensures that the depth of any tree remains small, making unionByRank also run in \( O(\alpha(n)) \).

• Processing Edges:

  Each edge is processed once, and both find and unionByRank operations are performed per edge. Since there are \( n \) edges, the overall time complexity is \( O(n \alpha(n)) \), which is nearly linear.

Space Complexity:

• Parent and Rank Arrays:

  We maintain two arrays: parent and rank, each of size \( O(n) \).

• Extra Space:

  No additional data structures are used apart from the input graph representation.

• Overall Space Complexity:

  The total space complexity is \( O(n) \), since we store parent and rank information for each node.