773. Sliding Puzzle

On an 2 x 3 board, there are five tiles labeled from 1 to 5, and an empty square represented by 0. A move consists of choosing 0 and a 4-directionally adjacent number and swapping it.

The state of the board is solved if and only if the board is [[1,2,3],[4,5,0]].

Given the puzzle board board, return the least number of moves required so that the state of the board is solved. If it is impossible for the state of the board to be solved, return -1.

Example 1:

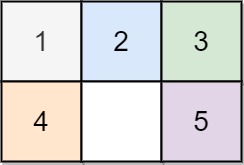
Input: board = [[1,2,3],[4,0,5]]
Output: 1
Explanation: Swap the 0 and the 5 in one move.

Example 2:

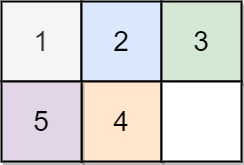
Input: board = [[1,2,3],[5,4,0]]
Output: -1
Explanation: No number of moves will make the board solved.

Example 3:

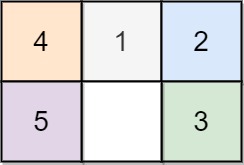
Input: board = [[4,1,2],[5,0,3]]
Output: 5
Explanation: 5 is the smallest number of moves that solves the board.
An example path:
After move 0: [[4,1,2],[5,0,3]]
After move 1: [[4,1,2],[0,5,3]]
After move 2: [[0,1,2],[4,5,3]]
After move 3: [[1,0,2],[4,5,3]]
After move 4: [[1,2,0],[4,5,3]]
After move 5: [[1,2,3],[4,5,0]]

Constraints:

• board.length == 2
• board[i].length == 3
• 0 <= board[i][j] <= 5
• Each value board[i][j] is unique.

Approach 01:

#include <vector>
#include <string>
#include <queue>
#include <unordered_set>
#include <array>
#include <algorithm>
using namespace std;

class Solution {
 public:
  int slidingPuzzle(vector<vector<int>>& board) {
    constexpr array<array<int, 2>, 4> directions = {{{0, 1}, {1, 0}, {0, -1}, {-1, 0}}};
    constexpr int rows = 2;
    constexpr int cols = 3;
    const string targetState = "123450";
    string initialState;

    // Convert the 2D board into a string representation
    for (int row = 0; row < rows; ++row)
      for (int col = 0; col < cols; ++col)
        initialState += '0' + board[row][col];

    if (initialState == targetState)
      return 0;

    queue<string> stateQueue{{initialState}};
    unordered_set<string> visitedStates{initialState};

    for (int steps = 1; !stateQueue.empty(); ++steps) {
      for (int currentLevelSize = stateQueue.size(); currentLevelSize > 0; --currentLevelSize) {
        string currentState = stateQueue.front();
        stateQueue.pop();
        const int zeroIndex = currentState.find('0');
        const int zeroRow = zeroIndex / cols;
        const int zeroCol = zeroIndex % cols;

        for (const auto& [dx, dy] : directions) {
          const int newRow = zeroRow + dx;
          const int newCol = zeroCol + dy;

          if (newRow < 0 || newRow >= rows || newCol < 0 || newCol >= cols)
            continue;

          const int swapIndex = newRow * cols + newCol;
          swap(currentState[zeroIndex], currentState[swapIndex]);

          if (currentState == targetState)
            return steps;

          if (!visitedStates.count(currentState)) {
            stateQueue.push(currentState);
            visitedStates.insert(currentState);
          }

          swap(currentState[zeroIndex], currentState[swapIndex]);
        }
      }
    }

    return -1;
  }
};

from collections import deque

class Solution:
    def slidingPuzzle(self, board):
        directions = [(0, 1), (1, 0), (0, -1), (-1, 0)]
        rows, cols = 2, 3
        targetState = "123450"
        initialState = ''.join(str(board[row][col]) for row in range(rows) for col in range(cols))

        if initialState == targetState:
            return 0

        stateQueue = deque([initialState])
        visitedStates = {initialState}

        steps = 0
        while stateQueue:
            steps += 1
            for _ in range(len(stateQueue)):
                currentState = stateQueue.popleft()
                zeroIndex = currentState.index('0')
                zeroRow, zeroCol = divmod(zeroIndex, cols)

                for dx, dy in directions:
                    newRow, newCol = zeroRow + dx, zeroCol + dy

                    if newRow < 0 or newRow >= rows or newCol < 0 or newCol >= cols:
                        continue

                    swapIndex = newRow * cols + newCol
                    nextState = list(currentState)
                    nextState[zeroIndex], nextState[swapIndex] = nextState[swapIndex], nextState[zeroIndex]
                    nextState = ''.join(nextState)

                    if nextState == targetState:
                        return steps

                    if nextState not in visitedStates:
                        stateQueue.append(nextState)
                        visitedStates.add(nextState)

        return -1

Time Complexity

• Total States:

  There are 6 tiles (numbers 0–5), which can be arranged in \( 6! = 720 \) unique configurations. However, only half of these are solvable due to parity constraints, so the effective total states are \( 720 / 2 = 360 \).

• BFS Traversal:

  BFS explores each state exactly once, and for each state, it processes all possible moves of the empty tile. Since there are at most 4 possible moves per state, the time complexity is proportional to \( O(4 \times 360) = O(1440) \), which simplifies to \( O(1) \) because the state space is bounded.

• Overall Time Complexity:

  \( O(1) \) due to the constant number of valid states.

Space Complexity

• Queue:

  The queue stores up to \( 360 \) states in the worst case, each represented as a string of 6 characters. This requires \( O(360 \times 6) = O(2160) = O(1) \) space.

• Visited Set:

  The visited set also stores up to \( 360 \) states, requiring \( O(360 \times 6) = O(2160) = O(1) \) space.

• Additional Space:

  Other variables (e.g., directions, temporary strings) require constant space \( O(1) \).

• Overall Space Complexity:

  \( O(1) \) due to the bounded state space and constant space overhead.