There is a directed graph of n nodes with each node labeled from 0 to n - 1. The graph is represented by a 0-indexed 2D integer array graph where graph[i] is an integer array of nodes adjacent to node i, meaning there is an edge from node i to each node in graph[i].
A node is a terminal node if there are no outgoing edges. A node is a safe node if every possible path starting from that node leads to a terminal node (or another safe node).
Return an array containing all the safe nodes of the graph. The answer should be sorted in ascending order.
Example 1:
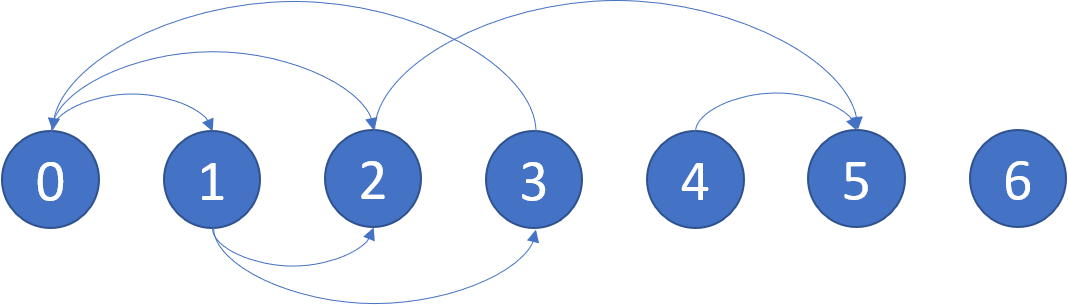
Input: graph = [[1,2],[2,3],[5],[0],[5],[],[]] Output: [2,4,5,6] Explanation: The given graph is shown above. Nodes 5 and 6 are terminal nodes as there are no outgoing edges from either of them. Every path starting at nodes 2, 4, 5, and 6 all lead to either node 5 or 6.
Example 2:
Input: graph = [[1,2,3,4],[1,2],[3,4],[0,4],[]] Output: [4] Explanation: Only node 4 is a terminal node, and every path starting at node 4 leads to node 4.
Constraints:
n == graph.length1 <= n <= 1040 <= graph[i].length <= n0 <= graph[i][j] <= n - 1graph[i]is sorted in a strictly increasing order.- The graph may contain self-loops.
- The number of edges in the graph will be in the range
[1, 4 * 104].
Approach 01:
-
C++
-
Python
enum class NodeState { unvisited, visiting, visited };
class Solution {
public:
vector<int> eventualSafeNodes(vector<vector<int>>& graph) {
vector<int> safeNodes; // Stores the eventual safe nodes
vector<NodeState> nodeStates(graph.size(), NodeState::unvisited); // Track the state of each node
for (int currentNode = 0; currentNode < graph.size(); ++currentNode)
if (!hasCycle(graph, currentNode, nodeStates))
safeNodes.push_back(currentNode);
return safeNodes;
}
private:
// Function to detect if a cycle exists starting from the given node
bool hasCycle(const vector<vector<int>>& graph, int currentNode, vector<NodeState>& nodeStates) {
if (nodeStates[currentNode] == NodeState::visiting) // Cycle detected
return true;
if (nodeStates[currentNode] == NodeState::visited) // Already processed node
return false;
nodeStates[currentNode] = NodeState::visiting; // Mark as visiting
for (const int neighbor : graph[currentNode]) // Explore all neighbors
if (hasCycle(graph, neighbor, nodeStates))
return true;
nodeStates[currentNode] = NodeState::visited; // Mark as fully visited
return false;
}
};
from enum import Enum
class NodeState(Enum):
UNVISITED = 0
VISITING = 1
VISITED = 2
class Solution:
def eventualSafeNodes(self, graph):
safeNodes = [] # Stores the eventual safe nodes
nodeStates = [NodeState.UNVISITED] * len(graph) # Track the state of each node
for currentNode in range(len(graph)):
if not self.hasCycle(graph, currentNode, nodeStates):
safeNodes.append(currentNode)
return safeNodes
def hasCycle(self, graph, currentNode, nodeStates):
if nodeStates[currentNode] == NodeState.VISITING: # Cycle detected
return True
if nodeStates[currentNode] == NodeState.VISITED: # Already processed node
return False
nodeStates[currentNode] = NodeState.VISITING # Mark as visiting
for neighbor in graph[currentNode]: # Explore all neighbors
if self.hasCycle(graph, neighbor, nodeStates):
return True
nodeStates[currentNode] = NodeState.VISITED # Mark as fully visited
return False
Time Complexity:
- DFS Traversal:
Each node is visited at most once during the depth-first search. For each node, we process all its neighbors, resulting in a time complexity proportional to the number of edges in the graph.
- Total Time Complexity:
The total time complexity is \( O(V + E) \), where \( V \) is the number of vertices (nodes) and \( E \) is the number of edges in the graph.
Space Complexity:
- Auxiliary Space:
The algorithm uses a
nodeStatesvector of size \( V \) to track the state of each node, resulting in \( O(V) \) space. - Recursive Stack Space:
The depth of the recursion stack can go up to \( O(V) \) in the worst case for a graph structured as a linear chain.
- Total Space Complexity:
The total space complexity is \( O(V) \).