A 3 x 3 magic square is a 3 x 3 grid filled with distinct numbers from 1 to 9 such that each row, column, and both diagonals all have the same sum.
Given a row x col grid of integers, how many 3 x 3 contiguous magic square subgrids are there?
Note: while a magic square can only contain numbers from 1 to 9, grid may contain numbers up to 15.
Example 1:
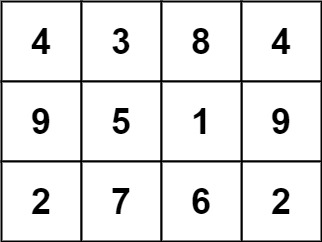
Input: grid = [[4,3,8,4],[9,5,1,9],[2,7,6,2]] Output: 1 Explanation: The following subgrid is a 3 x 3 magic square:while this one is not:
In total, there is only one magic square inside the given grid.
Example 2:
Input: grid = [[8]] Output: 0
Constraints:
row == grid.lengthcol == grid[i].length1 <= row, col <= 100 <= grid[i][j] <= 15
Approach 01:
Time Complexity
-
C++
-
Python
#include <vector>
#include <algorithm>
using namespace std;
class Solution {
public:
int numMagicSquaresInside(vector<vector<int>>& grid) {
int magicSquareCount = 0;
// Traverse through the grid, considering each 3x3 section
for (int row = 0; row + 2 < grid.size(); ++row) {
for (int col = 0; col + 2 < grid[0].size(); ++col) {
if (isMagicSquare(grid, row, col)) {
++magicSquareCount;
}
}
}
return magicSquareCount;
}
private:
// Function to check if a 3x3 section starting at (row, col) is a magic square
bool isMagicSquare(const vector<vector<int>>& grid, int row, int col) {
// Check that all values are between 1 and 9 and unique
vector<int> digits(10, 0);
for (int i = 0; i < 3; ++i) {
for (int j = 0; j < 3; ++j) {
int value = grid[row + i][col + j];
if (value < 1 || value > 9 || ++digits[value] > 1) {
return false;
}
}
}
// Check the sums of the rows, columns, and diagonals
int sum1 = grid[row][col] + grid[row][col + 1] + grid[row][col + 2];
int sum2 = grid[row + 1][col] + grid[row + 1][col + 1] + grid[row + 1][col + 2];
int sum3 = grid[row + 2][col] + grid[row + 2][col + 1] + grid[row + 2][col + 2];
int sum4 = grid[row][col] + grid[row + 1][col] + grid[row + 2][col];
int sum5 = grid[row][col + 1] + grid[row + 1][col + 1] + grid[row + 2][col + 1];
int sum6 = grid[row][col + 2] + grid[row + 1][col + 2] + grid[row + 2][col + 2];
int diagonal1 = grid[row][col] + grid[row + 1][col + 1] + grid[row + 2][col + 2];
int diagonal2 = grid[row][col + 2] + grid[row + 1][col + 1] + grid[row + 2][col];
// Return true if all sums are equal
return (sum1 == sum2 && sum2 == sum3 &&
sum3 == sum4 && sum4 == sum5 &&
sum5 == sum6 && sum6 == diagonal1 &&
diagonal1 == diagonal2);
}
};
class Solution:
def numMagicSquaresInside(self, grid):
magicSquareCount = 0
# Traverse through the grid, considering each 3x3 section
for row in range(len(grid) - 2):
for col in range(len(grid[0]) - 2):
if self.isMagicSquare(grid, row, col):
magicSquareCount += 1
return magicSquareCount
# Function to check if a 3x3 section starting at (row, col) is a magic square
def isMagicSquare(self, grid, row, col):
# Check that all values are between 1 and 9 and unique
digits = [0] * 10
for i in range(3):
for j in range(3):
value = grid[row + i][col + j]
if value < 1 or value > 9 or digits[value] > 0:
return False
digits[value] += 1
# Check the sums of the rows, columns, and diagonals
sum1 = grid[row][col] + grid[row][col + 1] + grid[row][col + 2]
sum2 = grid[row + 1][col] + grid[row + 1][col + 1] + grid[row + 1][col + 2]
sum3 = grid[row + 2][col] + grid[row + 2][col + 1] + grid[row + 2][col + 2]
sum4 = grid[row][col] + grid[row + 1][col] + grid[row + 2][col]
sum5 = grid[row][col + 1] + grid[row + 1][col + 1] + grid[row + 2][col + 1]
sum6 = grid[row][col + 2] + grid[row + 1][col + 2] + grid[row + 2][col + 2]
diagonal1 = grid[row][col] + grid[row + 1][col + 1] + grid[row + 2][col + 2]
diagonal2 = grid[row][col + 2] + grid[row + 1][col + 1] + grid[row + 2][col]
# Return true if all sums are equal
return (sum1 == sum2 and sum2 == sum3 and
sum3 == sum4 and sum4 == sum5 and
sum5 == sum6 and sum6 == diagonal1 and
diagonal1 == diagonal2)
- Grid Traversal:
The algorithm traverses the grid to check each possible 3×3 sub-grid. If the grid has dimensions \( m \times n \), there are approximately \( (m-2) \times (n-2) \) 3×3 sub-grids to check. Therefore, the time complexity for grid traversal is \( O(m \times n) \).
- Checking Magic Square:
For each 3×3 sub-grid, the algorithm checks if it forms a magic square. The number of operations for this check is constant (independent of \( m \) and \( n \)), so the time complexity of this check is \( O(1) \).
- Total Time Complexity:
The overall time complexity of the algorithm is \( O(m \times n) \), where \( m \) is the number of rows and \( n \) is the number of columns in the grid.
Space Complexity
- Auxiliary Space:
The algorithm uses an auxiliary vector of size 10 to check the uniqueness of digits in the 3×3 sub-grid, which requires \( O(1) \) space. Additionally, a few integer variables are used to store intermediate results, which also require \( O(1) \) space.
- Overall Space Complexity:
The overall space complexity of the algorithm is \( O(1) \), as it does not depend on the size of the input grid and only uses a constant amount of extra space.
Approach 02:
-
C++
-
Python
#include <vector>
#include <string>
#include <algorithm>
using namespace std;
class Solution {
public:
int numMagicSquaresInside(vector<vector<int>>& grid) {
int magicSquareCount = 0;
// Traverse through the grid, considering each 3x3 section
for (int row = 0; row + 2 < grid.size(); ++row) {
for (int col = 0; col + 2 < grid[0].size(); ++col) {
// Check for basic properties: the center of the magic square must be 5
if (grid[row][col] % 2 == 0 && grid[row + 1][col + 1] == 5) {
magicSquareCount += isMagicSquare(grid, row, col);
}
}
}
return magicSquareCount;
}
private:
// Function to check if a 3x3 section starting at (row, col) is a magic square
int isMagicSquare(const vector<vector<int>>& grid, int row, int col) {
string squarePattern;
// Construct a string pattern based on the elements' positions in the grid
for (const int position : {0, 1, 2, 5, 8, 7, 6, 3}) {
squarePattern += to_string(grid[row + position / 3][col + position % 3]);
}
// Check if the pattern matches any of the two valid magic square patterns
return string("4381672943816729").find(squarePattern) != string::npos ||
string("9276183492761834").find(squarePattern) != string::npos;
}
};
class Solution:
def numMagicSquaresInside(self, grid):
magicSquareCount = 0
# Traverse through the grid, considering each 3x3 section
for row in range(len(grid) - 2):
for col in range(len(grid[0]) - 2):
# Check for basic properties: the center of the magic square must be 5
if grid[row][col] % 2 == 0 and grid[row + 1][col + 1] == 5:
magicSquareCount += self.isMagicSquare(grid, row, col)
return magicSquareCount
# Function to check if a 3x3 section starting at (row, col) is a magic square
def isMagicSquare(self, grid, row, col):
squarePattern = ""
# Construct a string pattern based on the elements' positions in the grid
for position in [0, 1, 2, 5, 8, 7, 6, 3]:
squarePattern += str(grid[row + position // 3][col + position % 3])
# Check if the pattern matches any of the two valid magic square patterns
return "4381672943816729".find(squarePattern) != -1 or \
"9276183492761834".find(squarePattern) != -1
Time Complexity
- Grid Traversal:
The algorithm traverses each possible 3×3 section in the grid. If the grid has dimensions \( n \times m \), there are \( (n – 2) \times (m – 2) \) possible 3×3 sections. For each section, the algorithm checks if it forms a magic square. Therefore, the time complexity of the grid traversal is \( O((n – 2) \times (m – 2)) \).
- Magic Square Check:
For each 3×3 section, the `isMagicSquare` function constructs a string pattern and checks it against two possible valid patterns. This operation takes constant time \( O(1) \). Since this check is performed for each possible 3×3 section, the total time complexity remains \( O((n – 2) \times (m – 2)) \).
- Overall Time Complexity:
The overall time complexity of the algorithm is \( O((n – 2) \times (m – 2)) \), which simplifies to \( O(n \times m) \).
Space Complexity
- Result Storage:
The algorithm uses a single integer variable `magicSquareCount` to store the number of magic squares found. This requires \( O(1) \) space.
- String Pattern Construction:
In the `isMagicSquare` function, a string `squarePattern` is constructed for each 3×3 section. Since this string has a fixed length, the space required for it is constant \( O(1) \).
- Overall Space Complexity:
The overall space complexity of the algorithm is \( O(1) \), as it only uses a constant amount of extra space.