2022. Convert 1D Array Into 2D Array

You are given a 0-indexed 1-dimensional (1D) integer array original, and two integers, m and n. You are tasked with creating a 2-dimensional (2D) array with  m rows and n columns using all the elements from original.

The elements from indices 0 to n - 1 (inclusive) of original should form the first row of the constructed 2D array, the elements from indices n to 2 * n - 1 (inclusive) should form the second row of the constructed 2D array, and so on.

Return an m x n 2D array constructed according to the above procedure, or an empty 2D array if it is impossible.

Example 1:

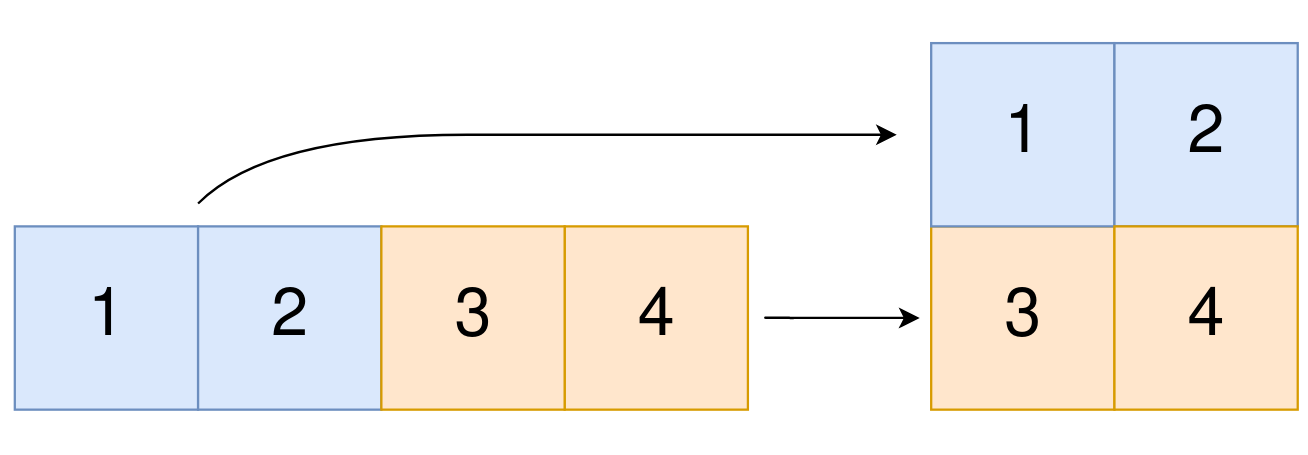
Input: original = [1,2,3,4], m = 2, n = 2
Output: [[1,2],[3,4]]
Explanation: The constructed 2D array should contain 2 rows and 2 columns.
The first group of n=2 elements in original, [1,2], becomes the first row in the constructed 2D array.
The second group of n=2 elements in original, [3,4], becomes the second row in the constructed 2D array.

Example 2:

Input: original = [1,2,3], m = 1, n = 3
Output: [[1,2,3]]
Explanation: The constructed 2D array should contain 1 row and 3 columns.
Put all three elements in original into the first row of the constructed 2D array.

Example 3:

Input: original = [1,2], m = 1, n = 1
Output: []
Explanation: There are 2 elements in original.
It is impossible to fit 2 elements in a 1x1 2D array, so return an empty 2D array.

Constraints:

• 1 <= original.length <= 5 * 104
• 1 <= original[i] <= 105
• 1 <= m, n <= 4 * 104

Approach 01:

class Solution {
  public:
    vector<vector<int>> construct2DArray(vector<int>& original, int m, int n) {
        vector<vector<int>> result;

        // Check if the size of the original array matches the 2D array dimensions
        if (original.size() != m * n) {
            return {};  // Return an empty array if the sizes do not match
        }

        // Construct the 2D array
        for (int i = 0; i < m; i++) {
            vector<int> row(original.begin() + (i * n), original.begin() + (i + 1) * n);
            result.push_back(row);
        }

        return result;
    }
};

class Solution:
    def construct2DArray(self, original: List[int], m: int, n: int) -> List[List[int]]:
        result = []
        if(len(original) != (m*n)):
            return []

        for i in range(m):
            result.append(original[(i*n):(i+1)*n])
        return result

Time Complexity

• Checking the Size:

  Verifying if the size of the original array matches the required size of the 2D array is an \( O(1) \) operation.

• Constructing the 2D Array:

  The solution uses a loop to create the 2D array from the original 1D array. This loop runs m times, and for each iteration, a subarray of size n is constructed using original.begin() + (i * n) and original.begin() + (i + 1) * n. Constructing each subarray takes \( O(n) \) time, making the total time complexity \( O(m \cdot n) \).

• Overall Time Complexity:

  The overall time complexity is \( O(m \cdot n) \), where m is the number of rows and n is the number of columns in the 2D array.

Space Complexity

• Space for Result:

  The solution uses an additional vector of vectors (result) to store the constructed 2D array. The space required for this result is \( O(m \cdot n) \) because it needs to store all the elements of the original array in a 2D format.

• Overall Space Complexity:

  The overall space complexity is \( O(m \cdot n) \), primarily due to the space required to store the result.