2807. Insert Greatest Common Divisors in Linked List

Given the head of a linked list head, in which each node contains an integer value.

Between every pair of adjacent nodes, insert a new node with a value equal to the greatest common divisor of them.

Return the linked list after insertion.

The greatest common divisor of two numbers is the largest positive integer that evenly divides both numbers.

Example 1:

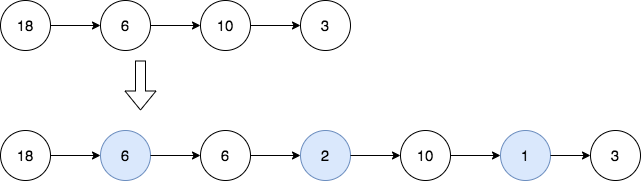
Input: head = [18,6,10,3]
Output: [18,6,6,2,10,1,3]
Explanation: The 1st diagram denotes the initial linked list and the 2nd diagram denotes the linked list after inserting the new nodes (nodes in blue are the inserted nodes).
- We insert the greatest common divisor of 18 and 6 = 6 between the 1st and the 2nd nodes.
- We insert the greatest common divisor of 6 and 10 = 2 between the 2nd and the 3rd nodes.
- We insert the greatest common divisor of 10 and 3 = 1 between the 3rd and the 4th nodes.
There are no more adjacent nodes, so we return the linked list.

Example 2:

Input: head = [7]
Output: [7]
Explanation: The 1st diagram denotes the initial linked list and the 2nd diagram denotes the linked list after inserting the new nodes.
There are no pairs of adjacent nodes, so we return the initial linked list.

Constraints:

• The number of nodes in the list is in the range [1, 5000].
• 1 <= Node.val <= 1000

Approach 01:

class Solution {
public:
    ListNode* insertGreatestCommonDivisors(ListNode* head) {
        // Traverse the linked list until the second-last node
        for (ListNode* currentNode = head; currentNode->next != nullptr;) {
            // Calculate the GCD of the current node's value and the next node's value
            int gcdValue = __gcd(currentNode->val, currentNode->next->val);
            
            // Create a new node with the GCD value, pointing to the next node
            ListNode* gcdNode = new ListNode(gcdValue, currentNode->next);
            
            // Insert the new GCD node between the current node and the next node
            currentNode->next = gcdNode;
            
            // Move to the node after the newly inserted GCD node
            currentNode = gcdNode->next;
        }
        
        return head;
    }
};

from math import gcd

class Solution:
    def insertGreatestCommonDivisors(self, head):
        # Traverse the linked list until the second-last node
        currentNode = head
        while currentNode and currentNode.next:
            # Calculate the GCD of the current node's value and the next node's value
            gcdValue = gcd(currentNode.val, currentNode.next.val)
            
            # Create a new node with the GCD value, pointing to the next node
            gcdNode = ListNode(gcdValue, currentNode.next)
            
            # Insert the new GCD node between the current node and the next node
            currentNode.next = gcdNode
            
            # Move to the node after the newly inserted GCD node
            currentNode = gcdNode.next

        return head

Time Complexity

• Traversing the Linked List:

  The algorithm traverses each node of the linked list once. Let n be the number of nodes in the original linked list. The loop runs approximately n times, making this operation \(O(n)\).

• Calculating GCD:

  The time complexity for calculating the greatest common divisor (GCD) of two numbers is \(O(\log(\min(a, b)))\), where a and b are the values of the current node and the next node, respectively. Since this operation is performed once for each pair of adjacent nodes, the complexity for all nodes is \(O(n \cdot \log(\min(a, b)))\). However, in practice, GCD calculation is very fast and can be considered constant time \(O(1)\) for most cases.

• Inserting New Nodes:

  Inserting a new node in the linked list is an \(O(1)\) operation. Since this operation is done for every node (except the last one), the complexity is \(O(n)\).

• Overall Time Complexity:

  The overall time complexity is \(O(n + n \cdot \log(\min(a, b)))\). Given that the GCD computation is fast, the time complexity is effectively \(O(n)\) in most practical cases.

Space Complexity

• Space for New Nodes:

  Each node in the linked list, except the last one, gets a new node inserted. This adds \(n – 1\) new nodes, leading to a space complexity of \(O(n)\) for the additional nodes.

• Space for GCD Calculation:

  Calculating the GCD requires a constant amount of extra space, \(O(1)\), since it only uses a few local variables.

• Overall Space Complexity:

  The overall space complexity is \(O(n)\) due to the newly inserted nodes in the linked list.