Multiply two linked lists

Given elements as nodes of the two singly linked lists. The task is to multiply these two linked lists, say L1 and L2.

Note: The output could be large take modulo 10⁹+7.

Examples :

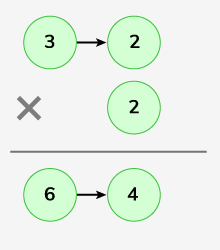
Input: LinkedList L1 : 3->2 , LinkedList L2 : 2
Output: 64
Explanation: 

Multiplication of 32 and 2 gives 64.

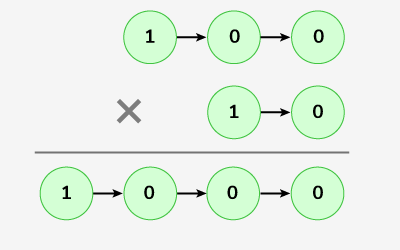
Input: LinkedList L1: 1->0->0 , LinkedList L2 : 1->0
Output: 1000
Explanation: 

Multiplication of 100 and 10 gives 1000.

Expected Time Complexity: O(max(n,m))
Expected Auxilliary Space: O(1)
where n is the size of L1 and m is the size of L2

Constraints:
1 <= number of nodes <= 9
0 <= node->data <= 9

Approach 01:

class solution {
public:
    long long multiplyTwoLists(Node* firstList, Node* secondList) {
        Node* currentNode = firstList;
        std::string firstNumberString;
        
        while (currentNode != nullptr) {
            int digit = currentNode->data;
            firstNumberString += std::to_string(digit);
            currentNode = currentNode->next;
        }
        
        long long firstNumber = std::stoll(firstNumberString);
        
        currentNode = secondList;
        std::string secondNumberString;
        
        while (currentNode != nullptr) {
            int digit = currentNode->data;
            secondNumberString += std::to_string(digit);
            currentNode = currentNode->next;
        }
        
        long long secondNumber = std::stoll(secondNumberString);
        
        const long long modValue = 1000000007LL;
        
        return ((firstNumber % modValue) * (secondNumber % modValue)) % modValue;
    }
};

class Solution:
    def multiply_two_lists(self, firstList: 'Node', secondList: 'Node') -> int:
        currentNode = firstList
        firstNumberString = ""
        
        while currentNode is not None:
            digit = currentNode.data
            firstNumberString += str(digit)
            currentNode = currentNode.next
        
        firstNumber = int(firstNumberString)
        
        currentNode = secondList
        secondNumberString = ""
        
        while currentNode is not None:
            digit = currentNode.data
            secondNumberString += str(digit)
            currentNode = currentNode.next
        
        secondNumber = int(secondNumberString)
        
        modValue = 1000000007
        
        return ((firstNumber % modValue) * (secondNumber % modValue)) % modValue

Time Complexity

• Traversing the first list:

  The algorithm traverses the entire first linked list to build the string representation of the number. If there are \(n_1\) nodes in the first list, this traversal takes \(O(n_1)\).

• Traversing the second list:

  The algorithm traverses the entire second linked list to build the string representation of the number. If there are \(n_2\) nodes in the second list, this traversal takes \(O(n_2)\).

• Converting strings to integers:

  The conversion of a string to a long long integer using std::stoll() takes \(O(n_1)\) and \(O(n_2)\) for the first and second lists, respectively, where \(n_1\) and \(n_2\) are the lengths of the number strings.

• Multiplication:

  Multiplying two long long integers takes constant time, \(O(1)\).

• Overall Time Complexity:

  The overall time complexity is \(O(n_1 + n_2)\), where \(n_1\) is the length of the first list and \(n_2\) is the length of the second list.

Space Complexity

• Auxiliary Space:

  Space is required for storing the string representations of the numbers. If the first list has \(n_1\) digits and the second list has \(n_2\) digits, the space used by the strings is \(O(n_1 + n_2)\). Additionally, the algorithm uses constant space for storing the final result and a few variables.

• Overall Space Complexity:

  The overall space complexity is \(O(n_1 + n_2)\), where \(n_1\) and \(n_2\) are the lengths of the first and second linked lists, respectively.