951. Flip Equivalent Binary Trees

For a binary tree T, we can define a flip operation as follows: choose any node, and swap the left and right child subtrees.

A binary tree X is flip equivalent to a binary tree Y if and only if we can make X equal to Y after some number of flip operations.

Given the roots of two binary trees root1 and root2, return true if the two trees are flip equivalent or false otherwise.

Example 1:

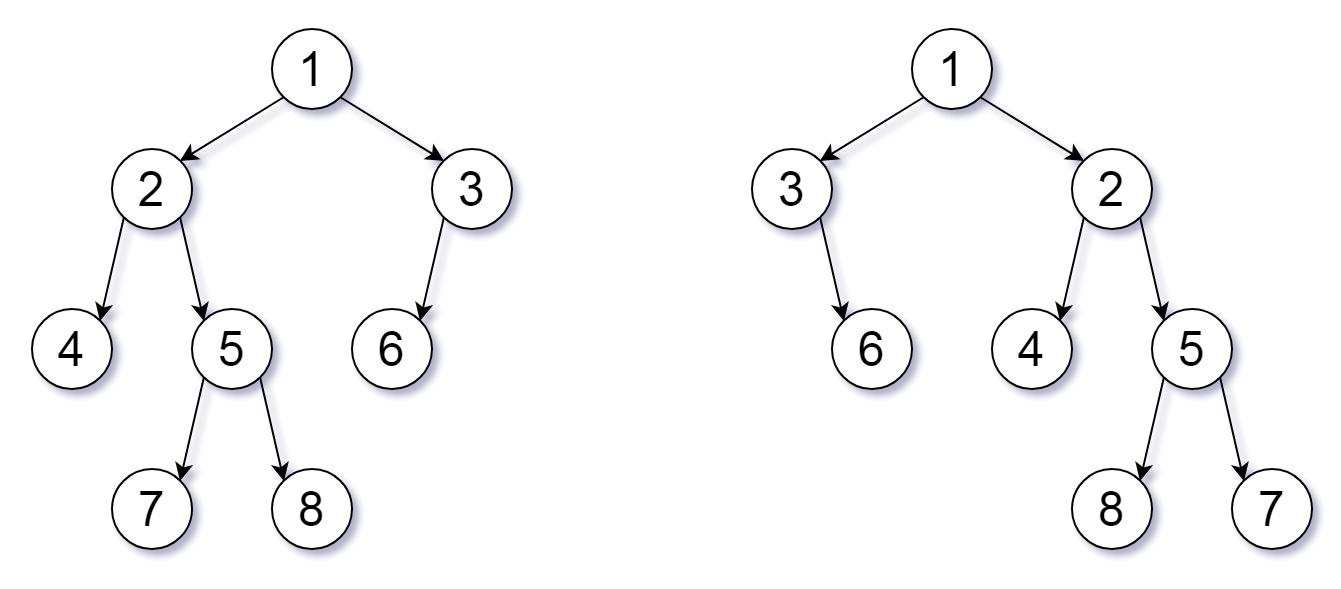
Input: root1 = [1,2,3,4,5,6,null,null,null,7,8], root2 = [1,3,2,null,6,4,5,null,null,null,null,8,7]
Output: true
Explanation: We flipped at nodes with values 1, 3, and 5.

Example 2:

Input: root1 = [], root2 = []
Output: true

Example 3:

Input: root1 = [], root2 = [1]
Output: false

Constraints:

• The number of nodes in each tree is in the range [0, 100].
• Each tree will have unique node values in the range [0, 99].

Approach 01:

class Solution {
public:
    bool flipEquiv(TreeNode* tree1, TreeNode* tree2) {
        if (tree1 == nullptr)
            return tree2 == nullptr;
        if (tree2 == nullptr)
            return tree1 == nullptr;
        if (tree1->val != tree2->val)
            return false;
        
        // Check for flip equivalence in both flipped and non-flipped scenarios
        return (flipEquiv(tree1->left, tree2->left) && 
                flipEquiv(tree1->right, tree2->right)) || 
               (flipEquiv(tree1->left, tree2->right) && 
                flipEquiv(tree1->right, tree2->left));
    }
};

class Solution:
    def flipEquiv(self, tree1: TreeNode, tree2: TreeNode) -> bool:
        if tree1 is None:
            return tree2 is None
        if tree2 is None:
            return tree1 is None
        if tree1.val != tree2.val:
            return False
        
        # Check for flip equivalence in both flipped and non-flipped scenarios
        return (self.flipEquiv(tree1.left, tree2.left) and 
                self.flipEquiv(tree1.right, tree2.right)) or \
               (self.flipEquiv(tree1.left, tree2.right) and 
                self.flipEquiv(tree1.right, tree2.left))

Time Complexity

• Recursive Traversal:

  The function recursively compares each node in both trees. In the worst case, it visits every node in both trees exactly once. Assuming both trees have n nodes, the time complexity is \(O(n)\), where n is the number of nodes in the larger of the two trees.

• Overall Time Complexity:

  The overall time complexity is \(O(n)\), where n is the number of nodes in the trees. Each recursive call compares the current nodes and then makes up to two recursive calls, one for each possible flip scenario.

Space Complexity

• Recursive Stack Space:

  The space complexity is determined by the maximum depth of the recursion stack, which corresponds to the height of the trees. In the worst case, the depth of the recursion is proportional to the height of the tree. For a balanced tree, this is \(O(\log n)\), and for a skewed tree, it can be as bad as \(O(n)\).

• Overall Space Complexity:

  The overall space complexity is \(O(h)\), where h is the height of the tree. In the worst case, this is \(O(n)\) for a skewed tree.