You are given a 0-indexed m x n matrix grid consisting of positive integers.
You can start at any cell in the first column of the matrix, and traverse the grid in the following way:
- From a cell
(row, col), you can move to any of the cells:(row - 1, col + 1),(row, col + 1)and(row + 1, col + 1)such that the value of the cell you move to, should be strictly bigger than the value of the current cell.
Return the maximum number of moves that you can perform.
Example 1:
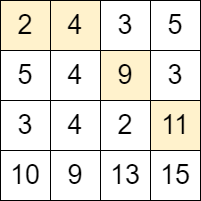
Input: grid = [[2,4,3,5],[5,4,9,3],[3,4,2,11],[10,9,13,15]] Output: 3 Explanation: We can start at the cell (0, 0) and make the following moves: - (0, 0) -> (0, 1). - (0, 1) -> (1, 2). - (1, 2) -> (2, 3). It can be shown that it is the maximum number of moves that can be made.
Example 2:
Input: grid = [[3,2,4],[2,1,9],[1,1,7]] Output: 0 Explanation: Starting from any cell in the first column we cannot perform any moves.
Constraints:
m == grid.lengthn == grid[i].length2 <= m, n <= 10004 <= m * n <= 1051 <= grid[i][j] <= 106
Approach 01:
-
C++
-
Python
class Solution {
public:
int maxMoves(vector<vector<int>>& grid) {
const int rows = grid.size();
const int cols = grid[0].size();
int maxMovesCount = 0;
// dp[i][j] represents the maximum number of moves you can perform from (i, j)
vector<vector<int>> maxMovesGrid(rows, vector<int>(cols));
for (int col = cols - 2; col >= 0; --col) {
for (int row = 0; row < rows; ++row) {
if (grid[row][col + 1] > grid[row][col])
maxMovesGrid[row][col] = 1 + maxMovesGrid[row][col + 1];
if (row > 0 && grid[row - 1][col + 1] > grid[row][col])
maxMovesGrid[row][col] = max(maxMovesGrid[row][col], 1 + maxMovesGrid[row - 1][col + 1]);
if (row + 1 < rows && grid[row + 1][col + 1] > grid[row][col])
maxMovesGrid[row][col] = max(maxMovesGrid[row][col], 1 + maxMovesGrid[row + 1][col + 1]);
}
}
for (int row = 0; row < rows; ++row)
maxMovesCount = max(maxMovesCount, maxMovesGrid[row][0]);
return maxMovesCount;
}
};
class Solution:
def maxMoves(self, grid: list[list[int]]) -> int:
rows = len(grid)
cols = len(grid[0])
maxMovesCount = 0
# maxMovesGrid[i][j] represents the maximum number of moves you can perform from (i, j)
maxMovesGrid = [[0] * cols for _ in range(rows)]
for col in range(cols - 2, -1, -1):
for row in range(rows):
if grid[row][col + 1] > grid[row][col]:
maxMovesGrid[row][col] = 1 + maxMovesGrid[row][col + 1]
if row > 0 and grid[row - 1][col + 1] > grid[row][col]:
maxMovesGrid[row][col] = max(maxMovesGrid[row][col], 1 + maxMovesGrid[row - 1][col + 1])
if row + 1 < rows and grid[row + 1][col + 1] > grid[row][col]:
maxMovesGrid[row][col] = max(maxMovesGrid[row][col], 1 + maxMovesGrid[row + 1][col + 1])
for row in range(rows):
maxMovesCount = max(maxMovesCount, maxMovesGrid[row][0])
return maxMovesCount
Time Complexity
- Grid Traversal:
We iterate over each cell in the grid, moving from the second-last column to the first column. This traversal requires \(O(\text{rows} \times \text{cols})\) time, where
rowsandcolsrepresent the number of rows and columns in the grid, respectively. - Move Calculation:
For each cell in the grid, the function checks up to three possible moves (right, upper-right, and lower-right). Each check is an
O(1)operation, so it does not affect the overall complexity. - Overall Time Complexity:
The overall time complexity is \(O(\text{rows} \times \text{cols})\).
Space Complexity
- Dynamic Programming (DP) Grid:
The
maxMovesGridvector stores the maximum moves from each cell, requiring \(O(\text{rows} \times \text{cols})\) space. - Auxiliary Storage:
Aside from the DP grid, only a few additional variables are used, resulting in constant extra space.
- Overall Space Complexity:
The space complexity is \(O(\text{rows} \times \text{cols})\).