Insert in Sorted way in a Sorted DLL

Given a sorted doubly linked list and an element x, you need to insert the element x into the correct position in the sorted Doubly linked list(DLL).

Note: The DLL is sorted in ascending order

Example:

Input: LinkedList: 3->5->8->10->12 , x = 9

Output: 3->5->8->9->10->12

Explanation: Here node 9 is inserted in the Doubly Linked-List.

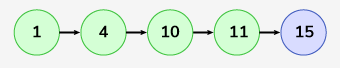
Input: LinkedList: 1->4->10->11 , x = 15

Output: 1->4->10->11->15

Constraints:
1 <= number of nodes <= 10³
1 <= node -> data , x <= 10⁴

Approach 01:

class Solution {
public:
    Node* sortedInsert(Node* head, int value) {
        Node* newNode = new Node;
        newNode->data = value;
        newNode->next = NULL;
        newNode->prev = NULL;
        
        if (head == NULL) {
            return newNode;
        }
        
        Node* current = head;

        // Insert at the beginning if the new node's value is smaller than the head's value
        if (current->data >= value) {
            newNode->next = head;
            head->prev = newNode;
            return newNode;
        }

        // Traverse to find the insertion point
        while (current->next != NULL && current->data < value) {
            current = current->next;
        }

        // Insert at the end if the current node's value is smaller than the new node's value
        if (current->data < value) {
            current->next = newNode;
            newNode->prev = current;
        } else {
            // Insert in the middle
            newNode->prev = current->prev;
            newNode->next = current;
            current->prev->next = newNode;
            current->prev = newNode;
        }

        return head;
    }
};

class Solution:
    def sortedInsert(self, head, value):
        newNode = Node(value)
        
        if head is None:
            return newNode
        
        current = head

        # Insert at the beginning if the new node's value is smaller than the head's value
        if current.data >= value:
            newNode.next = head
            head.prev = newNode
            return newNode

        # Traverse to find the insertion point
        while current.next is not None and current.data < value:
            current = current.next

        # Insert at the end if the current node's value is smaller than the new node's value
        if current.data < value:
            current.next = newNode
            newNode.prev = current
        else:
            # Insert in the middle
            newNode.prev = current.prev
            newNode.next = current
            current.prev.next = newNode
            current.prev = newNode

        return head

Time Complexity

• Insertion at the Beginning:

  If the new node has a value smaller than the current head node’s value, insertion happens in constant time, \(O(1)\).

• Traversal to Find the Insertion Point:

  In the worst case, the function may need to traverse the entire list to find the appropriate insertion point. This operation has a time complexity of \(O(n)\), where \(n\) is the number of nodes in the list.

• Insertion at the End or Middle:

  Once the correct position is found, inserting the new node has a constant time complexity of \(O(1)\).

• Overall Time Complexity:

  The overall time complexity is \(O(n)\), as the primary time-consuming step is traversing the list to find the correct insertion point.

Space Complexity

• Auxiliary Space for New Node:

  Creating a new node requires \(O(1)\) additional space.

• Overall Space Complexity:

  Since no additional data structures are used apart from the new node, the space complexity is \(O(1)\).