1975. Maximum Matrix Sum

You are given an n x n integer matrix. You can do the following operation any number of times:

• Choose any two adjacent elements of matrix and multiply each of them by -1.

Two elements are considered adjacent if and only if they share a border.

Your goal is to maximize the summation of the matrix’s elements. Return the maximum sum of the matrix’s elements using the operation mentioned above.

Example 1:

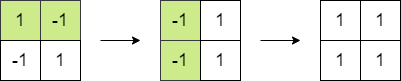
Input: matrix = [[1,-1],[-1,1]]
Output: 4
Explanation: We can follow the following steps to reach sum equals 4:
- Multiply the 2 elements in the first row by -1.
- Multiply the 2 elements in the first column by -1.

Example 2:

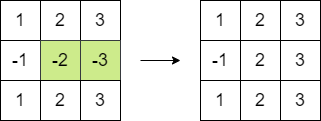
Input: matrix = [[1,2,3],[-1,-2,-3],[1,2,3]]
Output: 16
Explanation: We can follow the following step to reach sum equals 16:
- Multiply the 2 last elements in the second row by -1.

Constraints:

• n == matrix.length == matrix[i].length
• 2 <= n <= 250
• -105 <= matrix[i][j] <= 105

Approach 01:

#include <vector>
#include <algorithm>
#include <climits>
using namespace std;

class Solution {
 public:
  long long maxMatrixSum(vector<vector<int>>& matrix) {
    long long totalAbsoluteSum = 0;  // Total absolute value sum of elements
    int smallestAbsoluteValue = INT_MAX;  // Smallest absolute value in the matrix
    int isOddNegativeCount = 0;  // 0: Even number of negatives, 1: Odd number of negatives

    for (const vector<int>& row : matrix) {
      for (const int value : row) {
        totalAbsoluteSum += abs(value);
        smallestAbsoluteValue = min(smallestAbsoluteValue, abs(value));
        if (value < 0)
          isOddNegativeCount ^= 1;  // Toggle between 0 and 1
      }
    }

    // Subtract twice the smallest absolute value if the negative count is odd
    return totalAbsoluteSum - isOddNegativeCount * smallestAbsoluteValue * 2;
  }
};

from typing import List

class Solution:
    def maxMatrixSum(self, matrix: List[List[int]]) -> int:
        totalAbsoluteSum = 0  # Total absolute value sum of elements
        smallestAbsoluteValue = float('inf')  # Smallest absolute value in the matrix
        isOddNegativeCount = 0  # 0: Even number of negatives, 1: Odd number of negatives

        for row in matrix:
            for value in row:
                totalAbsoluteSum += abs(value)
                smallestAbsoluteValue = min(smallestAbsoluteValue, abs(value))
                if value < 0:
                    isOddNegativeCount ^= 1  # Toggle between 0 and 1

        # Subtract twice the smallest absolute value if the negative count is odd
        return totalAbsoluteSum - isOddNegativeCount * smallestAbsoluteValue * 2

Time Complexity

• Matrix Traversal:

  The function iterates through each element of the matrix exactly once. If the matrix has dimensions \( m \times n \), the total number of elements is \( m \times n \), leading to a time complexity of \( O(m \times n) \).

• Absolute Value Calculations:

  Calculating the absolute value, comparing it to find the minimum, and toggling the negative count are all \( O(1) \) operations per element, so they do not increase the complexity beyond \( O(m \times n) \).

• Overall Time Complexity:

  Since all operations are linear with respect to the number of elements, the overall time complexity is \( O(m \times n) \).

Space Complexity

• Variables:

  The function uses a constant number of scalar variables: totalAbsoluteSum, smallestAbsoluteValue, and isOddNegativeCount, which require \( O(1) \) space.

• Input Matrix:

  The input matrix matrix is not modified or duplicated, so it does not contribute to additional space usage.

• Overall Space Complexity:

  The overall space complexity is \( O(1) \), as no additional data structures are used.