Given two strings, one is a text string txt and the other is a pattern string pat. The task is to print the indexes of all the occurrences of the pattern string in the text string. Use 0-based indexing while returning the indices.
Note:Return an empty list in case of no occurrences of pattern.
Examples :
Input: txt = "abcab", pat = "ab" Output: [0, 3] Explanation: The string "ab" occurs twice in txt, one starts at index 0 and the other at index 3.
Input: txt = "abesdu", pat = "edu" Output: [] Explanation: There's no substring "edu" present in txt.
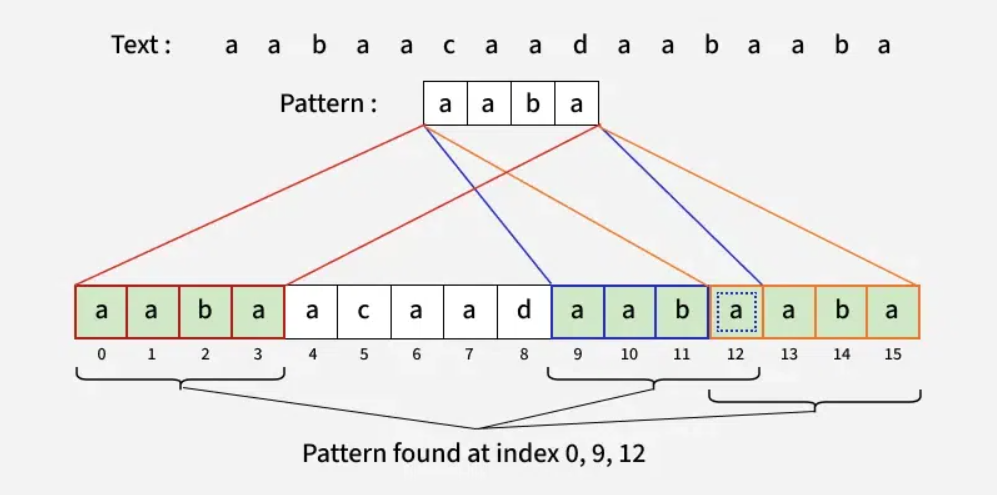
Input: txt = "aabaacaadaabaaba", pat = "aaba" Output: [0, 9, 12] Explanation:
Constraints:
1 ≤ txt.size() ≤ 106
1 ≤ pat.size() < txt.size()
Both the strings consist of lowercase English alphabets.
Approach 01:
-
C++
-
Python
class Solution {
public:
vector<int> computeLPSArray(string &pattern) {
int pattern_length = pattern.size();
vector<int> lps_array(pattern_length, 0);
int prefix_length = 0;
int current_index = 1;
while (current_index < pattern_length) {
if (pattern[current_index] == pattern[prefix_length]) {
prefix_length++;
lps_array[current_index] = prefix_length;
current_index++;
} else {
if (prefix_length != 0) {
prefix_length = lps_array[prefix_length - 1];
} else {
lps_array[current_index] = 0;
current_index++;
}
}
}
return lps_array;
}
vector<int> KMPAlgorithm(string &text, string &pattern) {
int pattern_length = pattern.size();
int text_length = text.size();
vector<int> lps_array = computeLPSArray(pattern);
vector<int> matching_indices;
int text_index = 0, pattern_index = 0;
while (text_index < text_length) {
if (pattern[pattern_index] == text[text_index]) {
text_index++;
pattern_index++;
}
if (pattern_index == pattern_length) {
matching_indices.push_back(text_index - pattern_index);
pattern_index = lps_array[pattern_index - 1];
} else if (text_index < text_length && pattern[pattern_index] != text[text_index]) {
if (pattern_index != 0) {
pattern_index = lps_array[pattern_index - 1];
} else {
text_index++;
}
}
}
return matching_indices;
}
vector<int> search(string pattern, string text) {
return KMPAlgorithm(text, pattern);
}
};
class Solution:
def computeLpsArray(self, pattern):
pattern_length = len(pattern)
lps_array = [0] * pattern_length
prefix_length = 0
current_index = 1
while current_index < pattern_length:
if pattern[current_index] == pattern[prefix_length]:
prefix_length += 1
lps_array[current_index] = prefix_length
current_index += 1
else:
if prefix_length != 0:
prefix_length = lps_array[prefix_length - 1]
else:
lps_array[current_index] = 0
current_index += 1
return lps_array
def kmpAlgorithm(self, text, pattern):
text_length = len(text)
pattern_length = len(pattern)
lps_array = self.computeLpsArray(pattern)
matching_indices = []
text_index, pattern_index = 0, 0
while text_index < text_length:
if pattern[pattern_index] == text[text_index]:
text_index += 1
pattern_index += 1
if pattern_index == pattern_length:
matching_indices.append(text_index - pattern_index)
pattern_index = lps_array[pattern_index - 1]
elif text_index < text_length and pattern[pattern_index] != text[text_index]:
if pattern_index != 0:
pattern_index = lps_array[pattern_index - 1]
else:
text_index += 1
return matching_indices
def search(self, pattern, text):
return self.kmpAlgorithm(text, pattern)
Time Complexity
- Computing the LPS array:
The
computeLPSArrayfunction iterates through the pattern once, using a two-pointer technique. Let the length of the pattern be \(M\). This step takes \(O(M)\). - Searching for matches:
The
KMPAlgorithmfunction iterates through the text while also incrementing or resetting the pattern pointer. Let the length of the text be \(N\). The two-pointer technique ensures that each character in the text and pattern is processed at most once, leading to \(O(N)\). - Overall Time Complexity:
The combined time complexity is \(O(M + N)\), as the LPS computation and the text search are performed sequentially.
Space Complexity
- LPS array:
The
computeLPSArrayfunction creates an LPS array of size \(M\), where \(M\) is the length of the pattern. This step uses \(O(M)\) space. - Matching indices:
The
KMPAlgorithmfunction stores the indices of matches in a vector, which in the worst case can have \(N\) entries if every character in the text matches the pattern. This step uses \(O(K)\) space, where \(K\) is the number of matches (bounded by \(N\)). - Overall Space Complexity:
The overall space complexity is \(O(M + K)\), where \(M\) is the length of the pattern and \(K\) is the number of matches in the text. In the worst case, this simplifies to \(O(M + N)\).