2661. First Completely Painted Row or Column

You are given a 0-indexed integer array arr, and an m x n integer matrix mat. arr and mat both contain all the integers in the range [1, m * n].

Go through each index i in arr starting from index 0 and paint the cell in mat containing the integer arr[i].

Return the smallest index i at which either a row or a column will be completely painted in mat.

Example 1:

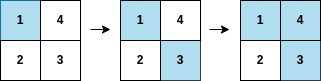
Input: arr = [1,3,4,2], mat = [[1,4],[2,3]]
Output: 2
Explanation: The moves are shown in order, and both the first row and second column of the matrix become fully painted at arr[2].

Example 2:

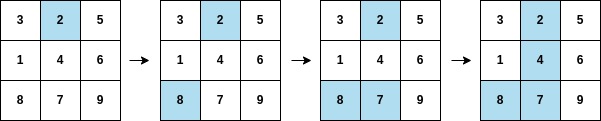
Input: arr = [2,8,7,4,1,3,5,6,9], mat = [[3,2,5],[1,4,6],[8,7,9]]
Output: 3
Explanation: The second column becomes fully painted at arr[3].

Constraints:

• m == mat.length
• n = mat[i].length
• arr.length == m * n
• 1 <= m, n <= 105
• 1 <= m * n <= 105
• 1 <= arr[i], mat[r][c] <= m * n
• All the integers of arr are unique.
• All the integers of mat are unique.

Approach 01:

class Solution {
public:
    int firstCompleteIndex(vector<int>& paintOrder, vector<vector<int>>& matrix) {
        const int numRows = matrix.size();
        const int numCols = matrix[0].size();

        // paintedRows[i]: the count of painted cells in the i-th row
        vector<int> paintedRows(numRows);
        // paintedCols[j]: the count of painted cells in the j-th column
        vector<int> paintedCols(numCols);
        // cellToRow[cellValue]: the row index of cellValue in the matrix
        vector<int> cellToRow(numRows * numCols + 1);
        // cellToCol[cellValue]: the column index of cellValue in the matrix
        vector<int> cellToCol(numRows * numCols + 1);

        // Map each cell value to its corresponding row and column in the matrix
        for (int row = 0; row < numRows; ++row) {
            for (int col = 0; col < numCols; ++col) {
                cellToRow[matrix[row][col]] = row;
                cellToCol[matrix[row][col]] = col;
            }
        }

        // Process the painting order and track row/column completion
        for (int index = 0; index < paintOrder.size(); ++index) {
            int row = cellToRow[paintOrder[index]];
            int col = cellToCol[paintOrder[index]];

            if (++paintedRows[row] ==
                numCols) // Check if the row is completely painted
                return index;
            if (++paintedCols[col] ==
                numRows) // Check if the column is completely painted
                return index;
        }

        throw; // This should not happen as the problem guarantees a valid solution
    }
};

class Solution:
    def firstCompleteIndex(self, paintOrder: list[int], matrix: list[list[int]]) -> int:
        numRows = len(matrix)
        numCols = len(matrix[0])
        
        # paintedRows[i]: the count of painted cells in the i-th row
        paintedRows = [0] * numRows
        # paintedCols[j]: the count of painted cells in the j-th column
        paintedCols = [0] * numCols
        # cellToRow[cellValue]: the row index of cellValue in the matrix
        cellToRow = [0] * (numRows * numCols + 1)
        # cellToCol[cellValue]: the column index of cellValue in the matrix
        cellToCol = [0] * (numRows * numCols + 1)

        # Map each cell value to its corresponding row and column in the matrix
        for row in range(numRows):
            for col in range(numCols):
                cellToRow[matrix[row][col]] = row
                cellToCol[matrix[row][col]] = col

        # Process the painting order and track row/column completion
        for index, cellValue in enumerate(paintOrder):
            row = cellToRow[cellValue]
            col = cellToCol[cellValue]
            
            paintedRows[row] += 1  # Increment the count for the row
            paintedCols[col] += 1  # Increment the count for the column
            
            if paintedRows[row] == numCols:  # Check if the row is completely painted
                return index
            if paintedCols[col] == numRows:  # Check if the column is completely painted
                return index

        raise RuntimeError("A valid solution is guaranteed, this should not occur.")

Time Complexity:

• Mapping Matrix Cells:

  To map each cell value in the matrix to its corresponding row and column, we traverse the entire matrix. This takes \( O(m \times n) \), where \( m \) is the number of rows and \( n \) is the number of columns.

• Processing the Painting Order:

  We iterate through the painting order, which has a length of \( p \), and for each cell, we perform constant-time operations such as updating counters and checking completion conditions. This takes \( O(p) \).

• Overall Time Complexity:

  The total time complexity is \( O(m \times n + p) \), where \( p \) is the size of the painting order.

Space Complexity:

• Auxiliary Space:

  We use:

  • A vector paintedRows of size \( m \).
  • A vector paintedCols of size \( n \).
  • Two vectors cellToRow and cellToCol of size \( m \times n + 1 \).
• Overall Space Complexity:

  The total space complexity is \( O(m \times n) \).