2017. Grid Game

You are given a 0-indexed 2D array grid of size 2 x n, where grid[r][c] represents the number of points at position (r, c) on the matrix. Two robots are playing a game on this matrix.

Both robots initially start at (0, 0) and want to reach (1, n-1). Each robot may only move to the right ((r, c) to (r, c + 1)) or down ((r, c) to (r + 1, c)).

At the start of the game, the first robot moves from (0, 0) to (1, n-1), collecting all the points from the cells on its path. For all cells (r, c) traversed on the path, grid[r][c] is set to 0. Then, the second robot moves from (0, 0) to (1, n-1), collecting the points on its path. Note that their paths may intersect with one another.

The first robot wants to minimize the number of points collected by the second robot. In contrast, the second robot wants to maximize the number of points it collects. If both robots play optimally, return the number of points collected by the second robot.

Example 1:

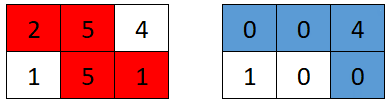
Input: grid = [[2,5,4],[1,5,1]]
Output: 4
Explanation: The optimal path taken by the first robot is shown in red, and the optimal path taken by the second robot is shown in blue.
The cells visited by the first robot are set to 0.
The second robot will collect 0 + 0 + 4 + 0 = 4 points.

Example 2:

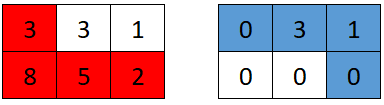
Input: grid = [[3,3,1],[8,5,2]]
Output: 4
Explanation: The optimal path taken by the first robot is shown in red, and the optimal path taken by the second robot is shown in blue.
The cells visited by the first robot are set to 0.
The second robot will collect 0 + 3 + 1 + 0 = 4 points.

Example 3:

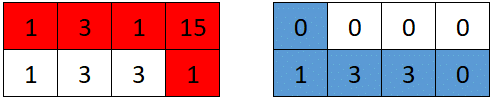
Input: grid = [[1,3,1,15],[1,3,3,1]]
Output: 7
Explanation: The optimal path taken by the first robot is shown in red, and the optimal path taken by the second robot is shown in blue.
The cells visited by the first robot are set to 0.
The second robot will collect 0 + 1 + 3 + 3 + 0 = 7 points.

Constraints:

• grid.length == 2
• n == grid[r].length
• 1 <= n <= 5 * 104
• 1 <= grid[r][c] <= 105

Approach 01:

class Solution {
public:
    long long gridGame(vector<vector<int>>& grid) {
        const int numCols = grid[0].size(); // Number of columns in the grid
        long minPoints = LONG_MAX; // Minimum points robot 2 can collect
        long upperRowSum = accumulate(grid[0].begin(), grid[0].end(), 0L); // Total points in the upper row
        long lowerRowSum = 0;              // Points collected in the lower row

        // Iterate through each column as the split point
        for (int col = 0; col < numCols; ++col) {
            upperRowSum -= grid[0][col]; // Deduct the points collected from the upper row
            // Calculate the maximum points robot 2 can collect at this split point
            minPoints = min(minPoints, max(upperRowSum, lowerRowSum));
            lowerRowSum +=
                grid[1][col]; // Add the points collected from the lower row
        }

        return minPoints;
    }
};

class Solution:
    def gridGame(self, grid: list[list[int]]) -> int:
        numCols = len(grid[0])  # Number of columns in the grid
        minPoints = float('inf')  # Minimum points robot 2 can collect
        upperRowSum = sum(grid[0])  # Total points in the upper row
        lowerRowSum = 0  # Points collected in the lower row

        # Iterate through each column as the split point
        for col in range(numCols):
            upperRowSum -= grid[0][col]  # Deduct the points collected from the upper row
            # Calculate the maximum points robot 2 can collect at this split point
            minPoints = min(minPoints, max(upperRowSum, lowerRowSum))
            lowerRowSum += grid[1][col]  # Add the points collected from the lower row

        return minPoints

Time Complexity:

• Upper Row Sum Calculation:

  The accumulate function computes the sum of the upper row, which takes \( O(C) \), where \( C \) is the number of columns in the grid.

• Iterating Through Columns:

  We iterate over each column to determine the split point, which also takes \( O(C) \).

• Overall Time Complexity:

  The total time complexity is \( O(C) \).

Space Complexity:

• Auxiliary Space:

  Only a few variables (upperRowSum, lowerRowSum, etc.) are used for computation, which results in \( O(1) \) additional space usage.

• Overall Space Complexity:

  The total space complexity is \( O(1) \).