802. Find Eventual Safe States

There is a directed graph of n nodes with each node labeled from 0 to n - 1. The graph is represented by a 0-indexed 2D integer array graph where graph[i] is an integer array of nodes adjacent to node i, meaning there is an edge from node i to each node in graph[i].

A node is a terminal node if there are no outgoing edges. A node is a safe node if every possible path starting from that node leads to a terminal node (or another safe node).

Return an array containing all the safe nodes of the graph. The answer should be sorted in ascending order.

Example 1:

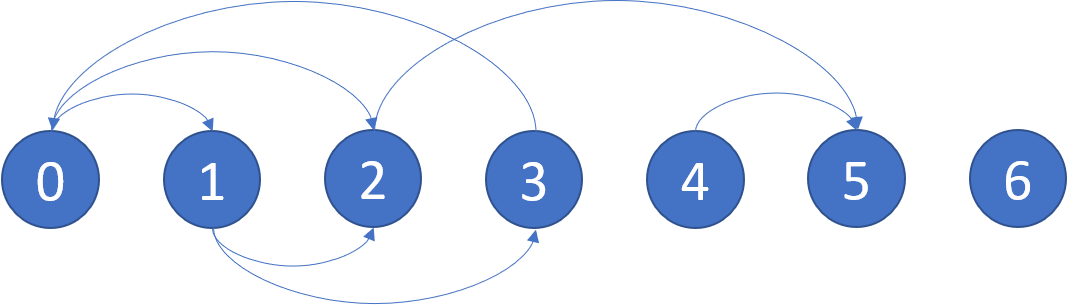
Input: graph = [[1,2],[2,3],[5],[0],[5],[],[]]
Output: [2,4,5,6]
Explanation: The given graph is shown above.
Nodes 5 and 6 are terminal nodes as there are no outgoing edges from either of them.
Every path starting at nodes 2, 4, 5, and 6 all lead to either node 5 or 6.

Example 2:

Input: graph = [[1,2,3,4],[1,2],[3,4],[0,4],[]]
Output: [4]
Explanation:
Only node 4 is a terminal node, and every path starting at node 4 leads to node 4.

Constraints:

• n == graph.length
• 1 <= n <= 104
• 0 <= graph[i].length <= n
• 0 <= graph[i][j] <= n - 1
• graph[i] is sorted in a strictly increasing order.
• The graph may contain self-loops.
• The number of edges in the graph will be in the range [1, 4 * 104].

Approach 01:

enum class NodeState { unvisited, visiting, visited };

class Solution {
public:
    vector<int> eventualSafeNodes(vector<vector<int>>& graph) {
        vector<int> safeNodes;                    // Stores the eventual safe nodes
        vector<NodeState> nodeStates(graph.size(), NodeState::unvisited);  // Track the state of each node

        for (int currentNode = 0; currentNode < graph.size(); ++currentNode)
            if (!hasCycle(graph, currentNode, nodeStates))
                safeNodes.push_back(currentNode);

        return safeNodes;
    }

private:
    // Function to detect if a cycle exists starting from the given node
    bool hasCycle(const vector<vector<int>>& graph, int currentNode, vector<NodeState>& nodeStates) {
        if (nodeStates[currentNode] == NodeState::visiting)  // Cycle detected
            return true;
        if (nodeStates[currentNode] == NodeState::visited)  // Already processed node
            return false;

        nodeStates[currentNode] = NodeState::visiting;  // Mark as visiting
        for (const int neighbor : graph[currentNode])   // Explore all neighbors
            if (hasCycle(graph, neighbor, nodeStates))
                return true;

        nodeStates[currentNode] = NodeState::visited;  // Mark as fully visited
        return false;
    }
};

from enum import Enum

class NodeState(Enum):
    UNVISITED = 0
    VISITING = 1
    VISITED = 2

class Solution:
    def eventualSafeNodes(self, graph):
        safeNodes = []  # Stores the eventual safe nodes
        nodeStates = [NodeState.UNVISITED] * len(graph)  # Track the state of each node

        for currentNode in range(len(graph)):
            if not self.hasCycle(graph, currentNode, nodeStates):
                safeNodes.append(currentNode)

        return safeNodes

    def hasCycle(self, graph, currentNode, nodeStates):
        if nodeStates[currentNode] == NodeState.VISITING:  # Cycle detected
            return True
        if nodeStates[currentNode] == NodeState.VISITED:  # Already processed node
            return False

        nodeStates[currentNode] = NodeState.VISITING  # Mark as visiting
        for neighbor in graph[currentNode]:           # Explore all neighbors
            if self.hasCycle(graph, neighbor, nodeStates):
                return True

        nodeStates[currentNode] = NodeState.VISITED  # Mark as fully visited
        return False

Time Complexity:

• DFS Traversal:

  Each node is visited at most once during the depth-first search. For each node, we process all its neighbors, resulting in a time complexity proportional to the number of edges in the graph.

• Total Time Complexity:

  The total time complexity is \( O(V + E) \), where \( V \) is the number of vertices (nodes) and \( E \) is the number of edges in the graph.

Space Complexity:

• Auxiliary Space:

  The algorithm uses a nodeStates vector of size \( V \) to track the state of each node, resulting in \( O(V) \) space.

• Recursive Stack Space:

  The depth of the recursion stack can go up to \( O(V) \) in the worst case for a graph structured as a linear chain.

• Total Space Complexity:

  The total space complexity is \( O(V) \).