A company is organizing a meeting and has a list of n employees, waiting to be invited. They have arranged for a large circular table, capable of seating any number of employees.
The employees are numbered from 0 to n - 1. Each employee has a favorite person and they will attend the meeting only if they can sit next to their favorite person at the table. The favorite person of an employee is not themself.
Given a 0-indexed integer array favorite, where favorite[i] denotes the favorite person of the ith employee, return the maximum number of employees that can be invited to the meeting.
Example 1:
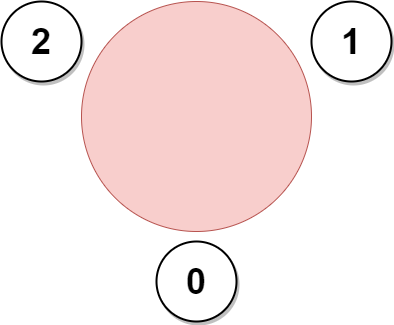
Input: favorite = [2,2,1,2] Output: 3 Explanation: The above figure shows how the company can invite employees 0, 1, and 2, and seat them at the round table. All employees cannot be invited because employee 2 cannot sit beside employees 0, 1, and 3, simultaneously. Note that the company can also invite employees 1, 2, and 3, and give them their desired seats. The maximum number of employees that can be invited to the meeting is 3.
Example 2:
Input: favorite = [1,2,0] Output: 3 Explanation: Each employee is the favorite person of at least one other employee, and the only way the company can invite them is if they invite every employee. The seating arrangement will be the same as that in the figure given in example 1: - Employee 0 will sit between employees 2 and 1. - Employee 1 will sit between employees 0 and 2. - Employee 2 will sit between employees 1 and 0. The maximum number of employees that can be invited to the meeting is 3.
Example 3:
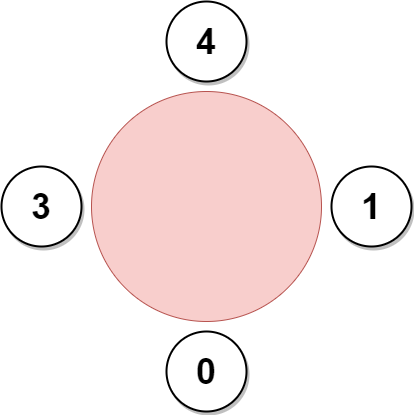
Input: favorite = [3,0,1,4,1] Output: 4 Explanation: The above figure shows how the company will invite employees 0, 1, 3, and 4, and seat them at the round table. Employee 2 cannot be invited because the two spots next to their favorite employee 1 are taken. So the company leaves them out of the meeting. The maximum number of employees that can be invited to the meeting is 4.
Constraints:
n == favorite.length2 <= n <= 1050 <= favorite[i] <= n - 1favorite[i] != i
Approach 01:
-
C++
-
Python
#include <vector>
#include <queue>
#include <unordered_set>
using namespace std;
enum class State { kInit, kVisiting, kVisited };
class Solution {
public:
int maximumInvitations(vector<int>& favorite) {
const int numPeople = favorite.size();
int totalComponentLength = 0; // Length of all 2-cycle components.
vector<vector<int>> adjacencyList(numPeople);
vector<int> inDegrees(numPeople, 0);
vector<int> longestChainLength(numPeople, 1);
// Build the graph using the favorite list.
for (int person = 0; person < numPeople; ++person) {
int likedPerson = favorite[person];
adjacencyList[person].push_back(likedPerson);
++inDegrees[likedPerson];
}
// Perform topological sorting to calculate maximum chain lengths.
queue<int> processingQueue;
for (int person = 0; person < numPeople; ++person) {
if (inDegrees[person] == 0) {
processingQueue.push(person);
}
}
while (!processingQueue.empty()) {
int currentPerson = processingQueue.front();
processingQueue.pop();
for (int neighbor : adjacencyList[currentPerson]) {
--inDegrees[neighbor];
if (inDegrees[neighbor] == 0) {
processingQueue.push(neighbor);
}
longestChainLength[neighbor] = max(longestChainLength[neighbor], 1 + longestChainLength[currentPerson]);
}
}
// Calculate the total length of all 2-cycle components.
for (int person = 0; person < numPeople; ++person) {
if (favorite[favorite[person]] == person) {
// Found a 2-cycle: person <-> favorite[person].
totalComponentLength += longestChainLength[person] + longestChainLength[favorite[person]];
}
}
int maxCycleLength = 0; // Longest cycle in the graph.
vector<int> parent(numPeople, -1);
unordered_set<int> visitedNodes;
vector<State> nodeStates(numPeople, State::kInit);
// Helper function to find the length of a cycle.
auto findCycle = [&](int node, auto&& findCycleRef) -> void {
visitedNodes.insert(node);
nodeStates[node] = State::kVisiting;
for (int neighbor : adjacencyList[node]) {
if (visitedNodes.find(neighbor) == visitedNodes.end()) {
parent[neighbor] = node;
findCycleRef(neighbor, findCycleRef);
} else if (nodeStates[neighbor] == State::kVisiting) {
// Found a cycle, calculate its length.
int currentNode = node;
int cycleLength = 1;
while (currentNode != neighbor) {
currentNode = parent[currentNode];
++cycleLength;
}
maxCycleLength = max(maxCycleLength, cycleLength);
}
}
nodeStates[node] = State::kVisited;
};
// Start DFS from every unvisited node to detect cycles.
for (int person = 0; person < numPeople; ++person) {
if (visitedNodes.find(person) == visitedNodes.end()) {
findCycle(person, findCycle);
}
}
return max(totalComponentLength / 2, maxCycleLength);
}
};
from enum import Enum
import collections
class State(Enum):
kInit = 0
kVisiting = 1
kVisited = 2
class Solution:
def maximumInvitations(self, favorite: list[int]) -> int:
numPeople = len(favorite)
totalComponentLength = 0 # Length of all 2-cycle components.
adjacencyList = [[] for _ in range(numPeople)]
inDegrees = [0] * numPeople
longestChainLength = [1] * numPeople
# Build the graph using the favorite list.
for person, likedPerson in enumerate(favorite):
adjacencyList[person].append(likedPerson)
inDegrees[likedPerson] += 1
# Perform topological sorting to calculate maximum chain lengths.
queue = collections.deque([person for person, inDegree in enumerate(inDegrees) if inDegree == 0])
while queue:
currentPerson = queue.popleft()
for neighbor in adjacencyList[currentPerson]:
inDegrees[neighbor] -= 1
if inDegrees[neighbor] == 0:
queue.append(neighbor)
longestChainLength[neighbor] = max(longestChainLength[neighbor], 1 + longestChainLength[currentPerson])
# Calculate the total length of all 2-cycle components.
for person in range(numPeople):
if favorite[favorite[person]] == person:
# Found a 2-cycle: person <-> favorite[person].
totalComponentLength += longestChainLength[person] + longestChainLength[favorite[person]]
maxCycleLength = 0 # Longest cycle in the graph.
parent = [-1] * numPeople
visitedNodes = set()
nodeStates = [State.kInit] * numPeople
# Helper function to find the length of a cycle.
def findCycle(node: int) -> None:
nonlocal maxCycleLength
visitedNodes.add(node)
nodeStates[node] = State.kVisiting
for neighbor in adjacencyList[node]:
if neighbor not in visitedNodes:
parent[neighbor] = node
findCycle(neighbor)
elif nodeStates[neighbor] == State.kVisiting:
# Found a cycle, calculate its length.
currentNode = node
cycleLength = 1
while currentNode != neighbor:
currentNode = parent[currentNode]
cycleLength += 1
maxCycleLength = max(maxCycleLength, cycleLength)
nodeStates[node] = State.kVisited
# Start DFS from every unvisited node to detect cycles.
for person in range(numPeople):
if person not in visitedNodes:
findCycle(person)
return max(totalComponentLength // 2, maxCycleLength)
Time Complexity:
- Graph Construction:
Building the adjacency list and calculating in-degrees takes \( O(N) \), where \( N \) is the number of people.
- Topological Sorting:
Processing nodes with zero in-degrees involves a traversal of all edges, which takes \( O(E) \), where \( E \) is the number of edges. In this case, \( E \leq N \) because each person points to exactly one other person.
- Cycle Detection:
Performing DFS on all nodes to detect cycles takes \( O(N + E) \). Since \( E \leq N \), this simplifies to \( O(N) \).
- Total Time Complexity:
The overall time complexity is \( O(N) \), as all operations scale linearly with the number of people.
Space Complexity:
- Graph Representation:
The adjacency list requires \( O(N) \) space to store the graph.
- Auxiliary Structures:
The in-degrees array, longest chain lengths array, parent array, and node states array each require \( O(N) \) space.
- DFS Stack and Visited Set:
The visited set and DFS recursion stack require \( O(N) \) space in the worst case.
- Total Space Complexity:
The total space complexity is \( O(N) \), dominated by the storage for the adjacency list and auxiliary structures.