There are a total of numCourses courses you have to take, labeled from 0 to numCourses - 1. You are given an array prerequisites where prerequisites[i] = [ai, bi] indicates that you must take course ai first if you want to take course bi.
- For example, the pair
[0, 1]indicates that you have to take course0before you can take course1.
Prerequisites can also be indirect. If course a is a prerequisite of course b, and course b is a prerequisite of course c, then course a is a prerequisite of course c.
You are also given an array queries where queries[j] = [uj, vj]. For the jth query, you should answer whether course uj is a prerequisite of course vj or not.
Return a boolean array answer, where answer[j] is the answer to the jth query.
Example 1:

Input: numCourses = 2, prerequisites = [[1,0]], queries = [[0,1],[1,0]] Output: [false,true] Explanation: The pair [1, 0] indicates that you have to take course 1 before you can take course 0. Course 0 is not a prerequisite of course 1, but the opposite is true.
Example 2:
Input: numCourses = 2, prerequisites = [], queries = [[1,0],[0,1]] Output: [false,false] Explanation: There are no prerequisites, and each course is independent.
Example 3:
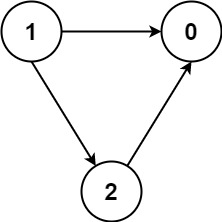
Input: numCourses = 3, prerequisites = [[1,2],[1,0],[2,0]], queries = [[1,0],[1,2]] Output: [true,true]
Constraints:
2 <= numCourses <= 1000 <= prerequisites.length <= (numCourses * (numCourses - 1) / 2)prerequisites[i].length == 20 <= ai, bi <= numCourses - 1ai != bi- All the pairs
[ai, bi]are unique. - The prerequisites graph has no cycles.
1 <= queries.length <= 1040 <= ui, vi <= numCourses - 1ui != vi
Approach 01:
-
C++
-
Python
class Solution {
public:
vector<bool> checkIfPrerequisite(int numCourses,
vector<vector<int>>& prerequisites,
vector<vector<int>>& queries) {
vector<bool> result;
// isPrerequisiteMatrix[i][j] := true if course i is a prerequisite of course j
vector<vector<bool>> isPrerequisiteMatrix(numCourses, vector<bool>(numCourses));
// Populate the initial prerequisites
for (const vector<int>& prerequisitePair : prerequisites) {
const int prerequisiteCourse = prerequisitePair[0];
const int dependentCourse = prerequisitePair[1];
isPrerequisiteMatrix[prerequisiteCourse][dependentCourse] = true;
}
// Use the Floyd-Warshall algorithm to determine all prerequisite relationships
for (int intermediateCourse = 0; intermediateCourse < numCourses; ++intermediateCourse)
for (int courseA = 0; courseA < numCourses; ++courseA)
for (int courseB = 0; courseB < numCourses; ++courseB)
isPrerequisiteMatrix[courseA][courseB] =
isPrerequisiteMatrix[courseA][courseB] ||
(isPrerequisiteMatrix[courseA][intermediateCourse] &&
isPrerequisiteMatrix[intermediateCourse][courseB]);
// Check each query
for (const vector<int>& queryPair : queries) {
const int courseA = queryPair[0];
const int courseB = queryPair[1];
result.push_back(isPrerequisiteMatrix[courseA][courseB]);
}
return result;
}
};
class Solution:
def checkIfPrerequisite(self, numCourses: int, prerequisites: List[List[int]], queries: List[List[int]]) -> List[bool]:
# isPrerequisiteMatrix[i][j] := True if course i is a prerequisite of course j
isPrerequisiteMatrix = [[False] * numCourses for _ in range(numCourses)]
# Populate the initial prerequisites
for prerequisitePair in prerequisites:
prerequisiteCourse = prerequisitePair[0]
dependentCourse = prerequisitePair[1]
isPrerequisiteMatrix[prerequisiteCourse][dependentCourse] = True
# Use the Floyd-Warshall algorithm to determine all prerequisite relationships
for intermediateCourse in range(numCourses):
for courseA in range(numCourses):
for courseB in range(numCourses):
isPrerequisiteMatrix[courseA][courseB] = (
isPrerequisiteMatrix[courseA][courseB]
or (
isPrerequisiteMatrix[courseA][intermediateCourse]
and isPrerequisiteMatrix[intermediateCourse][courseB]
)
)
# Check each query
result = []
for queryPair in queries:
courseA = queryPair[0]
courseB = queryPair[1]
result.append(isPrerequisiteMatrix[courseA][courseB])
return result
Time Complexity:
- Floyd-Warshall Algorithm:
The algorithm involves three nested loops, each iterating over the total number of courses, \( numCourses \). Thus, the time complexity for this part is \( O(numCourses^3) \).
- Processing Queries:
Each query is checked in \( O(1) \), and for \( q \) queries, this step has a time complexity of \( O(q) \).
- Overall Time Complexity:
The total time complexity is \( O(numCourses^3 + q) \), where \( q \) is the number of queries.
Space Complexity:
- Prerequisite Matrix:
The algorithm uses a \( numCourses \times numCourses \) matrix to store prerequisite relationships, resulting in a space complexity of \( O(numCourses^2) \).
- Auxiliary Space:
Other variables and data structures (e.g., vectors for the result) require \( O(q) \) space, where \( q \) is the number of queries.
- Overall Space Complexity:
The total space complexity is \( O(numCourses^2 + q) \).