2493. Divide Nodes Into the Maximum Number of Groups

You are given a positive integer n representing the number of nodes in an undirected graph. The nodes are labeled from 1 to n.

You are also given a 2D integer array edges, where edges[i] = [ai, bi] indicates that there is a bidirectional edge between nodes ai and bi. Notice that the given graph may be disconnected.

Divide the nodes of the graph into m groups (1-indexed) such that:

• Each node in the graph belongs to exactly one group.
• For every pair of nodes in the graph that are connected by an edge [ai, bi], if ai belongs to the group with index x, and bi belongs to the group with index y, then |y - x| = 1.

Return the maximum number of groups (i.e., maximum m) into which you can divide the nodes. Return -1 if it is impossible to group the nodes with the given conditions.

Example 1:

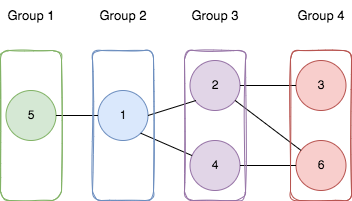
Input: n = 6, edges = [[1,2],[1,4],[1,5],[2,6],[2,3],[4,6]]
Output: 4
Explanation: As shown in the image we:
- Add node 5 to the first group.
- Add node 1 to the second group.
- Add nodes 2 and 4 to the third group.
- Add nodes 3 and 6 to the fourth group.
We can see that every edge is satisfied.
It can be shown that that if we create a fifth group and move any node from the third or fourth group to it, at least on of the edges will not be satisfied.

Example 2:

Input: n = 3, edges = [[1,2],[2,3],[3,1]]
Output: -1
Explanation: If we add node 1 to the first group, node 2 to the second group, and node 3 to the third group to satisfy the first two edges, we can see that the third edge will not be satisfied.
It can be shown that no grouping is possible.

Constraints:

• 1 <= n <= 500
• 1 <= edges.length <= 104
• edges[i].length == 2
• 1 <= ai, bi <= n
• ai != bi
• There is at most one edge between any pair of vertices.

Approach 01:

#include <vector>
#include <queue>
#include <unordered_map>
#include <numeric>
using namespace std;

class UnionFind {
 public:
  UnionFind(int size) : parent(size), rank(size) {
    iota(parent.begin(), parent.end(), 0);  // Initialize each node as its own parent
  }

  void unionByRank(int node1, int node2) {
    int root1 = find(node1);
    int root2 = find(node2);

    if (root1 == root2)
      return;

    // Union by rank
    if (rank[root1] < rank[root2]) {
      parent[root1] = root2;
    } else if (rank[root1] > rank[root2]) {
      parent[root2] = root1;
    } else {
      parent[root1] = root2;
      ++rank[root2];
    }
  }

  int find(int node) {
    return parent[node] == node ? node : parent[node] = find(parent[node]);  // Path compression
  }

 private:
  vector<int> parent;
  vector<int> rank;
};

class Solution {
 public:
  int magnificentSets(int numNodes, vector<vector<int>>& edges) {
    vector<vector<int>> adjacencyList(numNodes);
    UnionFind unionFind(numNodes);
    unordered_map<int, int> rootToMaxGroupSize;

    // Build adjacency list and perform union-find operations
    for (const vector<int>& edge : edges) {
      int node1 = edge[0] - 1;
      int node2 = edge[1] - 1;
      adjacencyList[node1].push_back(node2);
      adjacencyList[node2].push_back(node1);
      unionFind.unionByRank(node1, node2);
    }

    // Perform BFS to determine the maximum valid group size
    for (int i = 0; i < numNodes; ++i) {
      int maxGroupSize = bfs(adjacencyList, i);
      if (maxGroupSize == -1)
        return -1;  // Odd cycle detected

      int root = unionFind.find(i);
      rootToMaxGroupSize[root] = max(rootToMaxGroupSize[root], maxGroupSize);
    }

    int totalGroups = 0;
    for (const auto& [_, maxGroupSize] : rootToMaxGroupSize)
      totalGroups += maxGroupSize;

    return totalGroups;
  }

 private:
  int bfs(const vector<vector<int>>& adjacencyList, int startNode) {
    int depth = 0;
    queue<int> nodeQueue{{startNode}};
    unordered_map<int, int> nodeDepthMap{{startNode, 1}};

    while (!nodeQueue.empty()) {
      ++depth;
      for (int size = nodeQueue.size(); size > 0; --size) {
        int currentNode = nodeQueue.front();
        nodeQueue.pop();
        for (int neighbor : adjacencyList[currentNode]) {
          if (!nodeDepthMap.contains(neighbor)) {
            nodeQueue.push(neighbor);
            nodeDepthMap[neighbor] = depth + 1;
          } else if (nodeDepthMap[neighbor] == depth) {
            return -1;  // Odd-length cycle detected
          }
        }
      }
    }

    return depth;
  }
};

from collections import deque
from typing import List

class UnionFind:
    def __init__(self, size: int):
        self.parent = list(range(size))  # Initialize each node as its own parent
        self.rank = [0] * size  # Rank for union by rank optimization

    def unionByRank(self, node1: int, node2: int):
        root1 = self.find(node1)
        root2 = self.find(node2)

        if root1 == root2:
            return

        # Union by rank
        if self.rank[root1] < self.rank[root2]:
            self.parent[root1] = root2
        elif self.rank[root1] > self.rank[root2]:
            self.parent[root2] = root1
        else:
            self.parent[root1] = root2
            self.rank[root2] += 1

    def find(self, node: int) -> int:
        if self.parent[node] != node:
            self.parent[node] = self.find(self.parent[node])  # Path compression
        return self.parent[node]


class Solution:
    def magnificentSets(self, numNodes: int, edges: List[List[int]]) -> int:
        adjacencyList = [[] for _ in range(numNodes)]
        unionFind = UnionFind(numNodes)
        rootToMaxGroupSize = {}

        # Build adjacency list and perform union-find operations
        for node1, node2 in edges:
            node1 -= 1
            node2 -= 1
            adjacencyList[node1].append(node2)
            adjacencyList[node2].append(node1)
            unionFind.unionByRank(node1, node2)

        # Perform BFS to determine the maximum valid group size
        for i in range(numNodes):
            maxGroupSize = self.bfs(adjacencyList, i)
            if maxGroupSize == -1:
                return -1  # Odd cycle detected

            root = unionFind.find(i)
            rootToMaxGroupSize[root] = max(rootToMaxGroupSize.get(root, 0), maxGroupSize)

        return sum(rootToMaxGroupSize.values())

    def bfs(self, adjacencyList: List[List[int]], startNode: int) -> int:
        depth = 0
        nodeQueue = deque([startNode])
        nodeDepthMap = {startNode: 1}

        while nodeQueue:
            depth += 1
            for _ in range(len(nodeQueue)):
                currentNode = nodeQueue.popleft()
                for neighbor in adjacencyList[currentNode]:
                    if neighbor not in nodeDepthMap:
                        nodeQueue.append(neighbor)
                        nodeDepthMap[neighbor] = depth + 1
                    elif nodeDepthMap[neighbor] == depth:
                        return -1  # Odd-length cycle detected

        return depth

Time Complexity:

• Union-Find Operations:

  Each union and find operation runs in almost constant time due to path compression and union by rank, leading to an amortized complexity of \( O(\alpha(N)) \), where \( \alpha(N) \) is the inverse Ackermann function.

• Building the Adjacency List:

  Constructing the adjacency list takes \( O(E) \), where \( E \) is the number of edges.

• BFS Traversal:

  Each BFS traversal processes all nodes and edges, taking \( O(N + E) \).

• Overall Time Complexity:

  The dominant terms result in an overall complexity of \( O(N + E) \).

Space Complexity:

• Adjacency List Storage:

  Storing the graph takes \( O(N + E) \) space.

• Union-Find Data Structures:

  The parent and rank arrays require \( O(N) \) space.

• Additional Data Structures:

  The BFS queue and depth map take \( O(N) \) space in the worst case.

• Overall Space Complexity:

  The total space complexity is \( O(N + E) \).